Павел Васильев – самый тонкий лирик русской поэзии. Его стихи это яркое, стремительное и счастливое воображение, без которого не бывает большой поэзии. Его музыкальная сила поэтических строк Павла Васильева, затрагивает струны души
В стихах Васильева запечатлено множество состояний и оттенков любовной страсти – от стремительного и лёгкого полёта влюблённости до полнокровной, горячей и в то же время одухотворённой чувственности, есть в них жёсткий, плотский, на грани натурализма, но всегда это чувство сказочно, безоглядно-открыто, искренно . Стихи Васильева затрагивают самые потаенные струны души . Показывая то некое дежавю, читая его стихотворение сосздаеться обучение что все эти строки ты проживаешь сам.
Объяснение:
Перенесем все влево и вынесем за скобки  :
:
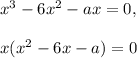
Из этого следует, что уравнение всегда имеет хотя бы одно решение -  . Задача сводится к тому, чтобы посмотреть, при каких
. Задача сводится к тому, чтобы посмотреть, при каких  будут корни у уравнения
будут корни у уравнения  и сколько их будет. Для этого достаточно рассмотреть 2 ситуации.
и сколько их будет. Для этого достаточно рассмотреть 2 ситуации.
1) проверим, при каком значении  корнем уравнения
корнем уравнения  будет
будет  . Подставляем ноль в уравнение:
. Подставляем ноль в уравнение: 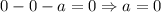 . При
. При  имеем:
имеем:

Делаем вывод, что при  уравнение имеет два корня:
уравнение имеет два корня: 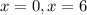 .
.
2) при 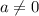 уравнение
уравнение  не может иметь корень
не может иметь корень  . Уравнение - квадратное. Сразу ищем дискриминант:
. Уравнение - квадратное. Сразу ищем дискриминант: 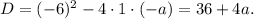
Здесь рассматриваем 3 случая:
2.1. Если  , то уравнение
, то уравнение  решений не имеет - следовательно, вторая скобка не будет давать новых решений и у исходного уравнения оно будет единственным.
решений не имеет - следовательно, вторая скобка не будет давать новых решений и у исходного уравнения оно будет единственным.
2.2. Если 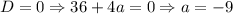 , то подставляя вместо параметра -9 в итоге получаем:
, то подставляя вместо параметра -9 в итоге получаем: 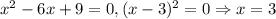 . Итого "вылез" еще один корень - значит, у исходного уравнения их будет два.
. Итого "вылез" еще один корень - значит, у исходного уравнения их будет два.
2.3. Если 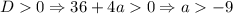 , то уравнение
, то уравнение  имеет два решения - следовательно, исходное будет иметь уже 3 решения. Заметим, что в это неравенство входит
имеет два решения - следовательно, исходное будет иметь уже 3 решения. Заметим, что в это неравенство входит  , а мы его проверяли отдельно - при
, а мы его проверяли отдельно - при  корней будет 2, а не 3, поэтому из неравенства его нужно исключить.
корней будет 2, а не 3, поэтому из неравенства его нужно исключить.
ОТВЕТ: При  уравнение имеет единственный корень; при
уравнение имеет единственный корень; при 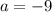 и
и  уравнение имеет два различных корня; при
уравнение имеет два различных корня; при 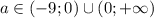 уравнение имеет три различных корня.
уравнение имеет три различных корня.
у - клены
{x+y=63
{1/5 x=1/2 y
{x=63-y
{0.2x=0.5y
0.2(63-y)=0.5y
12.6-0.2y-0.5y=0
-0.7y=-12.6
y=18
x=63-18=45
ответ: 45 тополей и 18 кленов.