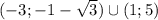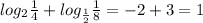
ответ:
объяснение:
здесь область допустимых значений состоит только из двух
под первым корнем квадратный трехчлен --парабола, ветви вверх:
2x²-8x+6 ≥ 0
x²-4x+3 ≥ 0 корни: 1 и 3 (по теореме виета)
решение: х ∈ (-∞; 1] u [3; +∞)
под вторым корнем квадратный трехчлен --парабола, ветви вниз:
-x²+4x-3 ≥ 0
x²-4x+3 ≤ 0 корни те же))
решение: х ∈ [1; 3]
пересечением этих двух промежутков (условия должны выполняться одновременно) будет множество из двух точек: х ∈ {1; 3}
легко проверить, что х=1 решением не является, т.к. сумма двух неотрицательных чисел (это квадратные корни) не может быть < 1-1 (меньше нуля)
остается х = 3: √0 + √0 < 3-1 это верно))
ответ: х=3
ОДЗ:
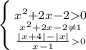
Решаем каждое неравенство:
 ⇒
⇒ 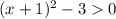 ⇒
⇒

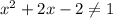 ⇒
⇒  ⇒
⇒ 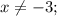
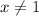

Подмодульные выражения обращаются в 0 в точках
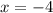 и
и 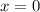
Это точки делят числовую прямую на три промежутка.
Раскрываем знак модуля на промежутках:
(-∞;-4]
|x+4|=-x-4
|x|=-x
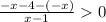 ⇒
⇒  ⇒ x < 1
⇒ x < 1
решение неравенства (-∞;-4]
(-4;0]
|x+4|=x+4
|x|=-x
 ⇒
⇒  ⇒ x < -2 или x > 1
⇒ x < -2 или x > 1
решение неравенства (-4;-2)
(0;+∞)
|x+4|=x+4
|x|=x
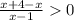 ⇒
⇒  ⇒ x > 1
⇒ x > 1
решение неравенства (1;+∞]
Объединяем ответы трех случаев:
 при
при 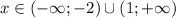
ОДЗ:

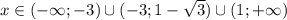
Решаем неравенство: 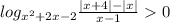
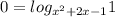
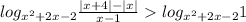
Два случая:
если основание логарифмической функции >1, то она возрастает и большему значению функции соответствует большее значение аргумента
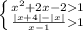 ⇒
⇒  ⇒
⇒ ![\left \{ {{x\in (-\infty;-3) \cup(1;+\infty)} \atop {x\in(-\infty;-4]\cup(1;5)}} \right.](/tpl/images/1360/8793/82812.png)
второе неравенство решаем на промежутках так:
(-∞;-4]
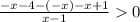 ⇒
⇒  ⇒
⇒ 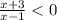 ⇒ (-3;-1)
⇒ (-3;-1)
не принадлежат (-∞;-4]
на (-4;0]
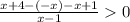 ⇒
⇒ 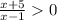 ⇒ x < -5 или x > 1
⇒ x < -5 или x > 1
не принадлежат (-4;0]
(0;+∞)
 ⇒
⇒ 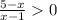 ⇒
⇒ 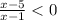 ⇒
⇒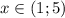
о т в е т этого случая 
если основание логарифмической функции 0 < a < 1, то она убывает и большему значению функции соответствует меньшее значение аргумента
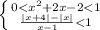 ⇒
⇒  ⇒
⇒ ![\left \{ {{x\in (-3;-1-\sqrt{3}) \cup(-1+\sqrt{3};1)} \atop {x\in(-\infty;-4]\cup(-4;0]\cup(5;+\infty)}} \right.](/tpl/images/1360/8793/ac205.png)
второе неравенство решаем на промежутках так:
(-∞;-4]
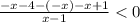 ⇒
⇒ 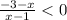 ⇒
⇒ 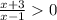 ⇒
⇒
(-∞;-3)U(1;+∞)
о т в е т. (-∞;-4]
на (-4;0]
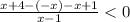 ⇒
⇒ 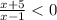 ⇒ -5 < x < 1
⇒ -5 < x < 1
о т в е т. (-4;0]
(0;+∞)
 ⇒
⇒ 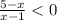 ⇒
⇒ 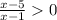 ⇒
⇒
о т в е т этого случая 
С учетом ОДЗ получаем окончательный ответ: