1)найдите общий вид первообразных для функции: 2) вычислите интегралы 3) найдите площадь фигуры ограниченной линиями, , 4)вычислите: 5) решите уравнение:
Четырёхзначное число "abcd" можно представить в виде: а*1000+b*100+c*10+d, при этом произведение а*b*c*d =10, соответственно данное число может состоять из цифр 1,1,2 и 5. Очевидно, что делимое при делении без остатка на 28 (кратное 28) может заканчиваться только на 2, т.к. произведение 8 с другими числами не может образовывать в разряде единиц ни 1, ни 5. Остается три варианта четырёхзначных чисел это 1152, 1512 и 5112, из которых на 28 делится только 1512 (это 54). 1512 - это единственный ответ.
Формула площади треугольника имеет вид: S=ab/2, где a - высота, b - основание. Примем формулу площади треугольника за функцию S(b), выразим a через b, чтобы функция была от одной независимой переменной b. Высоту a вычислим с т.Пифагора: a=√2²-(b/2)²= Подставляя полученное выражение в формулу функции S(b) вместо а получим: . Нужно найти значение переменной b такое, при котором функция S(b) примет наибольшее значение Найдем производную: Приравняем её к нулю и найдем точки экстремума, в одной из которых функция принимает искомое наибольшее значение: S(2√2)=2 S(-2√2)=-2 В точке b=2√2 функция S(b) принимает наибольшее значение. Т.о, основание треугольника должно быть равным 2√2, чтобы площадь треугольника была наибольшей.
1)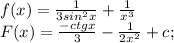
c є R
2)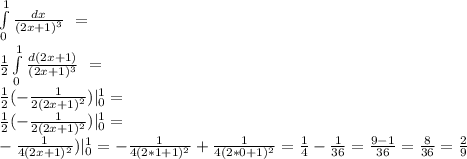
3) Ищем точки пересечения
точек пересечения нет, фигура неограничена, найти площадь не представляется возможным
4)![\sqrt[3] {-2\sqrt{2}}+\sqrt[6] {2}\sqrt [3]{2}=\\ \sqrt[3] {(-\sqrt{2})^3}+\sqrt[6] {2}\sqrt [6]{2^2}=\\ -\sqrt{2}+\sqrt[6] {2*2^2}=\\ -\sqrt{2}+\sqrt[6] {2^3}=\\ -\sqrt{2}+\sqrt {2}=0](/tpl/images/0106/8377/2ae85.png)
5)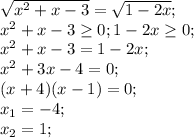
1-2*1<0 - корень 1 не подходит
-4 удовлетворяет
ответ: -4