х€(0; +оо)
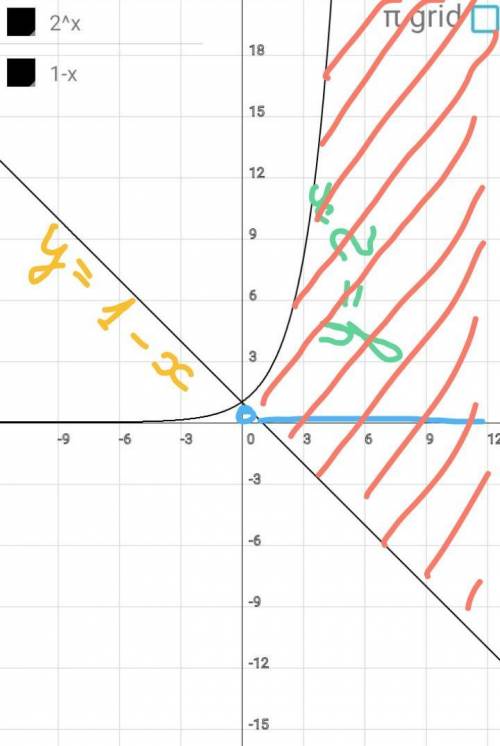
Графическое решение
неравенств.
Объяснение:
Шаг 1.
Строим график функции
у=2^х.
Показательная функция
а>1 ==> функция возрастает.
Пересекает ось ординат в
точке х=0.
у(0)=2^0=1
Шаг 2.
Строим график фцнкции
у=1-х или у=-х+1.
Линейная функция k<0
==> функция убывает.
Пересекает ось ординат в
точке х=0.
у(0)=0+1=1
Шаг 3.
В одной системе координат
строим графики функций
(по точкам).
Графики пересекаются в
точке (0; 1).
Шаг4.
Графически решаем задан
ное неравенство:
определяем участки, на кото
рых график функции у=2^х
расположен выше графика
функции у=-х+1.
х€(0; +оо).
х€(0; +оо)
С применением степени
(квадрат и куб) и дроби
(x^2 - 1)/(x^3 + 1)
Квадратный корень
sqrt(x)/(x + 1)
Кубический корень
cbrt(x)/(3*x + 2)
С применением синуса и косинуса
2*sin(x)*cos(x)
Арксинус
x*arcsin(x)
Арккосинус
x*arccos(x)
Применение логарифма
x*log(x, 10)
Натуральный логарифм
ln(x)/x
Экспонента
exp(x)*x
Тангенс
tg(x)*sin(x)
Котангенс
ctg(x)*cos(x)
Иррациональне дроби
(sqrt(x) - 1)/sqrt(x^2 - x - 1)
Арктангенс
x*arctg(x)
Арккотангенс
x*arсctg(x)
Гиберболические синус и косинус
2*sh(x)*ch(x)
Гиберболические тангенс и котангенс
ctgh(x)/tgh(x)
Гиберболические арксинус и арккосинус
x^2*arcsinh(x)*arccosh(x)
Гиберболические арктангенс и арккотангенс
x^2*arctgh(x)*arcctgh(x)
S/15 - время поездки на велосипеде
S/40-время поездки на автобусе. Получаем уравнение:
S/15-S/40=2.5
8S-3S=300
5S=300
S=60 (км)