Для того, чтобы выполнить упрощение выражений а) 2x - 3y - 11x + 8y; б) 5(2a + 1) - 3; в) 14x - (x - 1) + (2x + 6) мы с вами к каждому из заданных выражений применим алгоритм его упрощения.
Давайте вспомним алгоритм действий:
1. открытие скобок; 2. группировка и приведение подобных слагаемых.
В первом выражение нет скобок и мы переходим к приведению подобных сразу:
а) 2x - 3y - 11x + 8y = 2x - 11x + 8y - 3y = -9x + 5y;
б) 5(2a + 1) - 3 = 5 * 2a + 5 * 1 - 3 = 10a + 5 - 3 = 10a + 2;
в) 14x - (x - 1) + (2x + 6) = 14x - x + 1 + 2x + 6 = 14x - x + 2x + 1 + 6 = 15x + 7.
Объяснение:
.
Первое уравнение переделаем в следующий вид
Подставим значение из второго уравнения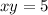 
в первое преобразованное уравнение, тогда получается
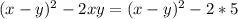
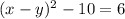
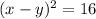
Здесь возможны два случая
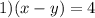и 
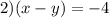
Получаются две системы уравнений.
1) решим первый случай
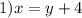
Подставляем во второе уравнение исходной системы
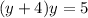
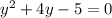
корнями уравнения будут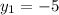 
, 
.
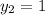Значит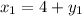 
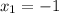
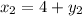
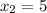
Двумя парами ответов будут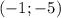 
и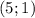 
.
2) решим второй случай
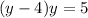
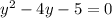
корнями уравнения будут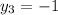 
, 
.
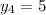Значит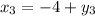 
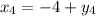
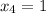
Двумя парами ответов будут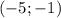 
и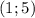 
.
Все решения проходят ОДЗ и при подстановке дают верные ответы
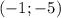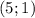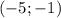ответ 4 пары решения и , и .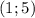
y=3-2x
x²+9x-6x²+9-12x+4x²-11=0
-x²-3x-2=0
x²+3x+2=0
x1+x2=-3 U x1*x2=2
x1=-2⇒y1=3+4=7
x2=-1⇒y2=3+2=5
(-2;7) U (-1;5)