Question

А1. запишите в виде выражения : а) сумму чисел 67,5 и 12,1; б) произведение числа 5,2 и разности чисел 7,8 и 15,6. а2. найдите значение выражения: а) -48: 12 +(124 230) б) 8 32 : (-8/13)x 0,26+ 15,6

Answer 1

Полное условие в приложении.

А1.

а) 67,5+12,1

б) 5,2·(7,8-15,6)

А2.

а)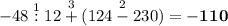 $\displaystyle -48\overset{1}{:} 12\overset{3}{+}(124\overset{2}{-}230)=\bold{-110}$

1) -48:12 = -4

2) 124-230 = -(230-124) = -106

3) -4+(-106) = -(4+106) = -110

б)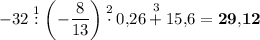 $\displaystyle -32\overset{1}{:}\left( -\dfrac8{13} \right) \overset{2}{\cdot }0,\! 26\overset{3}{+}15,\! 6=\bold{29,\! 12}$

1) $-32:\left( -\dfrac8{13}\right) =-4\cdot 8\cdot \dfrac{-13}8=4\cdot 13=52$

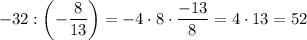
2) $52\cdot 0,\! 26=52\cdot \dfrac{26}{100}=\dfrac{1352}{100} =13,\! 52$

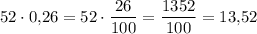
3) 13,52+15,6 = 13,52+15,60 = 29,12

A3.

При a=6 и b=3:

-a+4b-15 = -6+4·3-15 = -6+12-15 = 6-15 = -(15-6) = -9

A4.

8x руб. - стоимость 8 тетрадей по х рублей.

3y руб. - стоимость 3 учебников по y рублей.

8x+3y руб - вся покупка.

В1.

Дробь не имеет смысла, когда знаменатель равен нулю.

а) x+3 = 0;   x = -3

б) b(b-5) = 0;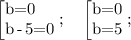   $\left[\begin{array}{}b=0\\b\,-\,5=0\end{array}\right.;\quad \left[\begin{array}{}b=0\\b=5\end{array}\right.;\quad$   b={0;5}