3³-2c²+3c-4-(c³-3c²-5)
для начала упростим выражение:
3³-2c²+3c-4-(c³-3c²-5)
раскрываем скобки
27-2с²+3с-4-с³+3с²+5=
изменяем порядок действий
-с³+(3с²-2с²)+3с+(27-4+5)=-с³+с²+3с+28
если c=2, то -с³+с²+3с+28=-2³+2²+3·2+28=-8+4+6+28=30
4x²-(2x³+4x²-5)
для начала упростим выражение:
раскрываем скобки
4x²-(2x³+4x²-5)=4х²-2х³-4х²+5=
изменяем порядок действий
-2х³+(4х²-4х²)+5=-2х³+5
если x=-3, то -2х³+5=-2·(-3)³+5=-2·(-27)+5=54+5=59
2p-(1-p²-p³)-(2p+p²-p³)
для начала упростим выражение:
раскрываем скобки
2p-(1-p²-p³)-(2p+p²-p³)=2р-1+р²+р³-2р-р²+р³=
изменяем порядок действий
(р³+р³)+(р²-р²)+(2р-2р)-1=2р³-1
если 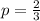 , то
, то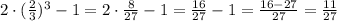
1. Алгебраическая дробь имеет смысл при любых значениях переменной, кроме тех, которые делают знаменатель равным нулю. В данном случае знаменатель первой дроби равен нулю при x=5 и x=-5, а знаменатель второй дроби равен нулю при y=4 и y=-4.
2. 14a³/21a⁴ = 2/3a
15x²/10x³ = 3/2x
3.
A) 2/3a + 1/a = (2a+a)/3a = 3a/3a = 1
B) 2x²/x²-4 - 2x/x+2 = 2x²(x+2)/x²-4(x+2) - 2x(x-2)/x²-4(x-2) = (2x³+4x²-2x³+8x)/(x²-4)(x+2) = (4x²+8x)/(x²-4)(x+2) = 4x(x+2)/(x+2)(x-2)(x+2) = 4x/(x-2)
C) 4/3в + 2/в = (4в+6)/3в = 2(2в+3)/3в
D) 3x²/x²-1 - 3x/x-1 = 3x(x-1)/(x+1)(x-1) - 3(x+1)/(x+1)(x-1) = (3x²-3x-3)/(x+1)(x-1) = 3(x²-x-1)/(x+1)(x-1)
5.
A) 8x/15y * 20y/16x = (8*20)/(15*16) = 2/3
B) в²-8в+16/2в+6 : в²-16/4в+12 = (в-4) / (в+4)
C) 6x/13y * 26y/18x = (6*26)/(13*18) = 2/3
D) 2x-4/x²+12x+36 : 8x-16/x²-36 = (2(x-2))/(x+6)(x+6) : 8(x-2)/(x+6)(x-6) = (2(x-2)* (x-6))/(8(x-2)) = (x-6)/4(x+9)
решение во вложении