На протяжении всей истории математики[⇨] представление о и допустимых методах доказательства существенно менялось, в основном, в сторону большей формализации и бо́льших ограничений. Ключевой вехой в вопросе формализации доказательства стало создание математической логики[⇨] в XIX веке и формализация её средствами основных техник доказательства. В XX веке построена теория доказательств — теория, изучающая доказательство как математический объект[⇨]. С появлением во второй половине XX века компьютеров особое значение получило применение методов математического доказательства для проверки и синтеза программ[⇨], и даже было установлено структурное соответствие между компьютерными программами и математическими доказательствами (соответствие Карри — Ховарда[⇨]), на основе которого созданы средства автоматического доказательства[⇨].
Объяснение:
Основные приёмы, используемые при построении доказательств: прямое доказательство[⇨], математическая индукция и её обобщения[⇨], доказательство от противного[⇨], контрапозиция[⇨], построение[⇨], перебор[⇨], установление биекции[⇨], двойной счёт[⇨]; в приложениях в качестве математических доказательств привлекаются также методы, не дающие формального доказательства, но обеспечивающие практическую применимость результата[⇨] — вероятностные, статистические, приближённые. В зависимости от раздела математики, используемого формализма или математической школы не все методы могут приниматься безоговорочно, в частности, конструктивное доказательство[⇨] предполагает серьёзные ограничения.
Объяснение:
1) 0,5·sin2x = sin35° ⇔ sin2x = 2·sin35° (1) ; так как y = sinx
возрастает в первой четверти , то sin35° > sin30° = 0,5 ⇒
2·sin35° > 1 ⇒ уравнение (1) не имеет решений
2) arcsin 2x = arccos x (2) , arccos x ≥ 0 для всех х ⇒ arcsin 2x ≥ 0
⇒ х ≥ 0 ; так как из области определения у = arcsin2x следует
, что х ≤ 0,5 , то уравнение (2) имеет решение только ,
если x ∈ [ 0 ; 0,5] , на этом отрезке левая часть уравнения
меняется от 0 до π/2 , а правая от π/3 до π/2 ⇒
уравнение ( 2) имеет решение , если множество
значений обеих частей не выходит за пределы [π/3 ; π/2] , но
на этом отрезке функция y = sinx - возрастает ⇒ уравнение ( 1 )
равносильно на [ 0 ; 0,5] следующему :
sin(arcsin2x) = sin(arccosx)
2x = 
⇔ 4x² = 1 - x² ⇔ x² = 1/5 ⇒
x =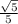 
( так как х ≥ 0)
функции , стоящие в левой и правой частях уравнения имеют
разную монотонность , поэтому сразу ясно , что уравнение
имеет не более одного корня , в этом случае его достаточно
" угадать " , но угадать не получилось , пришлось брать
синусы от обеих частей
f(x) = g(x) ⇔ h(f(x)) = h(g(x) ) , если h(x) - монотонна и значения
f и g входят в область определения функции h , поэтому
и пришлось доказывать , что значения f и g не выходят
за пределы первой четверти , а там синус возрастает и
поэтому законно брать синусы от обеих частей
tg² x - 4tg x + 3 = 0
Решаем как квадратное. По т. Виета
tg x = 3 tg x = 1
x = arctg 3 + πk, k∈Z x = π/4 + πn, n∈Z