

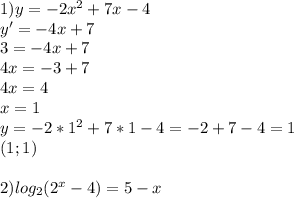
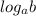 есть область допустимых значений (ОДЗ)
есть область допустимых значений (ОДЗ)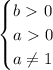
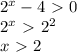
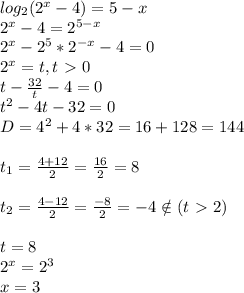
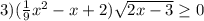
![\sqrt[2n]{a}\\a \geq 0](/tpl/images/0407/7919/72735.png)
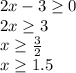
 войдет в ответ.
войдет в ответ.
![x\in(-\infty;3]U[6;+\infty)](/tpl/images/0407/7919/ea52c.png)
![x\in[1.5;3]U[6;+\infty)](/tpl/images/0407/7919/8f8e6.png)
нехай перший рухався зі швидкістю х км/год, а другий у км/год. тоді перший пройшов до зустрічі 3х км, а другий 3у км., а разом 3х+3у=27 км за умовою перший прийшов на 1 год 21 хв=1,35 год раніше. тому 27/у-27/х=1,35 складемо систему рівнянь [latex] \left \{ {3x+3y=27} \atop {27/y-27/x=1.35}} \right. [/latex] виразимо в першому рівнянні х через у х=9-у підставимо в друге рівняння 20х-20у=ху . маємо: 180-20у-20у=9у-у² у²-49у+180=0 d=1681 y1=(49+41)/2=45 y2=4 тоді x1=9-45=-36 , що не задов умові і х2=9-4=5 км/год швидкість першого пішохода 5 км/год, а другого 4 км/год
давайте решим два линейных неравенства 1) 5(3x - 5) > 3(1 + 5x) - 10, 2) 5(4x - 1) < 5(2x + 3) + 2x используя тождественные преобразования.
давайте начнем с открытия скобок в обеих частях неравенства:
1) 5(3x - 5) > 3(1 + 5x) - 10;
5 * 3x - 5 * 5 > 3 * 1 + 3 * 5x - 10;
15x - 25 > 3 + 15x - 10;
группируем подобные в разных частях неравенства:
15x - 15x > 3 - 10 + 25;
x(15 - 15) > 18;
0 > 18.
неравенство не верное, значит нет решения неравенства.
2) 5(4x - 1) < 5(2x + 3) + 2x;
20x - 5 < 10x + 15 + 2x;
20x - 10x - 2x < 15 + 5;
8x < 20;
x < 20 : 8;
x < 2.5.
x принадлежит промежутку (- бесконечность; 2,5).