![1)\; \; \frac{5}{1+\sqrt[3]{32\cdot (cos^215)^2-10-8\sqrt3}}=[\, cos^2 \alpha =\frac{1+cos2 \alpha }{2}\, ]=\\\\=\frac{5}{1+ \sqrt[3]{32\cdot (\frac{1+cos30}{2})^2-10-8\sqrt3} }=\frac{5}{1+\sqrt[3]{\frac{32}{4}\cdot (1+\frac{\sqrt3}{2})^2-10-8\sqrt3}}=\\\\=\frac{5}{1+\sqrt[3]{8\cdot (1+\sqrt3+\frac{3}{4})-10-8\sqrt3}}=\frac{5}{1+\sqrt[3]{8+8\sqrt3+6-10-8\sqrt3}}=\frac{5}{1+\sqrt[3]{4}}](/tpl/images/0408/6368/9724b.png)
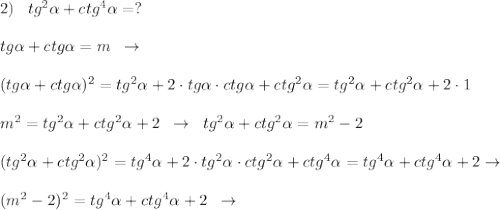
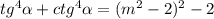
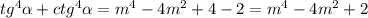
Пусть новая дневная норма равна Х га. С этой нормой фермер вспахал поле за 72/Х = Д (дней). (1)
Фермер превысил дневную норму на 9 га и вспахал поле на 4 дня раньше, то есть со старой нормой он бы вспахал поле за
72/(Х-9) = Д+4 (дней). (2).
Подставим значение (1) в уравнение (2) и получим:
72/(Х-9) = 72/Х + 4. Решаем уравнение:
72Х = 72(Х-9) +4Х(Х-9) => Х² - 9X - 162 = 0.
X1 = (9+√(81+648))/2 = (9+27)/2 = 18.
Х2 получается отрицательным и не удовлетворяет условиям задачи.
Итак, фермер вспахал все поле за 72/18 = 4 дня.