Основная теорема алгебры. Уравнение n-го степеня имеет n корней. Иными словами: каков старший степень - столько и корней (действительные и комплексные)
Решим к примеру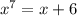 
уравнение в действительных корнях.
Рассмотрим функцию 
. Эта функция является возрастающей на всей числовой прямой.
Также рассмотрим правую часть уравнения: функцию 
. Графиком линейной функции является прямой, проходящей через точки (0;6), (-6;0).
графики пересекаются в одной точке, следовательно, уравнение имеет один действительный корень и 6 комплексно-сопряженные корни.
Возьмем теперь к примеру уравнение 
Если D>0, то квадратное уравнение имеет два ДЕЙСТВИТЕЛЬНЫХ корня.
Если D=0, то квадратное уравнение имеет два равные корни.
Если D<0, то квадратное уравнение действительных корня не имеет, но имеет два комплексно сопряженных корня.
Чтобы вычислить периметр необходимо найти 2 другие её стороны. Они будут равными, так как трапеция равнобедренная.
Для того, чтобы найти неизвестные стороны, рассмотрим треугольник, который получится при проведении высоты трапеции.
Неизвестная сторона является гипотенузой прямоугольного треугольника.
Нам известен угол, равный 60 град.
Косинус угла равен отношению прилежащего катета к к гипотенузе
cos 60град=1/2
Прилежащий катет равен: от большего основания отнимем меньшее найдём стороны катетов у двух прямоугольников, образовавшихся при проведении высоты на меньшее основание.
Сторона одного катета равна:
(49 -15) :2=34 :2=17
Одна из неизвестных сторон трапеции равна:
17/с=1/2
с=34
Периметр трапеции равен:
Р=15+49+2*34=132 (см)
ответ: 132см