
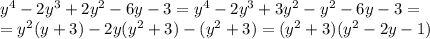
4x2−3x+1=0 ;
a=4 ;
b=−3 ;
c=1 .
Корни квадратного уравнения вычисляют по формулам:
x1 = −b+D−−√2⋅a ; x2 = −b−D−−√2⋅a , где D= b2−4ac .
D называется дискриминантом.
По значению дискриминанта можно определить количество корней квадратного уравнения.
Если D<0 (отрицательный), то у уравнения нет действительных корней.
Если D=0 , то у уравнения два равных корня.
Если D>0 (положительный), то у уравнения два различных корня.
Приведённое квадратное уравнение (коэффициент при x2 равен 1 , т. е. а=1 )
x2+bx+c=0 можно решить с теоремы Виета: {x1⋅x2=cx1+x2=−b
Неполные квадратные уравнения
Неполные квадратные уравнения имеют 2 вида:
1. если c=0 , то ax2+bx=0 ;
2. если b=0 , то ax2+c=0 .
Неполные квадратные уравнения можно решать с формул дискриминанта, но рациональнее выбрать специальные
1. ax2+bx=0 можно решить, разложив на множители (вынести за скобку x )
x⋅(ax+b)=0 .
x=0 или ax+b=0 . Значит, один корень равен 0 , а второй корень x=−ba
(т. к. произведение двух чисел равно 0 только тогда, когда хотя бы один из множителей равен 0 ).
2x2−30x=0;x(2x−30)=0;x=0,или2x−30=0;2x=30;x=15.
ответ: x=0 ; x=15 .
2. ax2+c=0 можно решить, извлекая корень из каждой части уравнения.
ax2=−c ; (обе стороны делятся на a ) x2=−ca .
|x|= −ca−−−√ . Извлекая корень из правой части уравнения, получаем x по модулю.
Это значит, что
x1 = −ca−−−√ ;
x2 = −−ca−−−√ .
4x2−100=0;4x2=100∣∣:4x2=25;|x|=25−−√;
из этого следует, что x=5 или x=−5 .
ответ: x1=5 ; x2=−5 .
x2+36=0;x2=−36.
У уравнения нет решения, т. к. квадратный корень из отрицательного числа не имеет смысла (также известно, что число во второй степени не может быть отрицательным).
ответ: корней нет.