Теорема: Если плоскость проходит через данную прямую, параллельную другой плоскости, и пересекает эту плоскость, то линия пересечения плоскостей параллельна данной прямой.
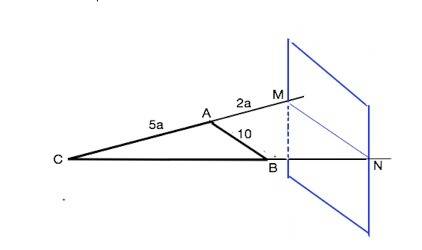
В данном случае плоскость, которой принадлежит ∆ АВС, проходит через АВ, параллельную другой плоскости и пересекает её, поэтому линия MN пересечения этих плоскостей параллельна АВ.
Плоскость, параллельная АВ, пересекает не сами стороны, а продолжения сторон АС и ВС, поэтому проходит вне треугольника, МС=АМ+АС, и МN > AB (см. рисунок)
Примем коэффициент отношения АМ:АС=а.
Тогда АС=5а, АМ=2а, а АМ=5а+2а=7а.
Плоскость параллельна АВ, следовательно, пересекает плоскость, в которой лежит треугольник, по прямой, параллельной АВ.
Соответственные углы при пересечении параллельных прямых АВ и MN секущими АМ и СN равны. ⇒ ∆ АВС~∆ AMN ( их углы равны).
Из подобия следует отношение:
АМ:АС=MN:AB
7a:5a=MN:10⇒
MN=70:5=14 (ед. длины)
Да можно
Объяснение:
1 ёмкость - А 700мл
2 ёмкость - В 800мл
3 ёмкость - С 0мл
В ёмкость А с ёмкости В переливаем 300мл получается в ёмкости А 1 литр а в ёмкости В 500мл и ёмкость С 0 мл
Затем в ёмкость В наливаем из ёмкости А 500мл и получаем в ёмкости В 1 литр перемешанного раствора и остаётся в ёмкости А 500мл и ёмкость С 0мл
Затем в ёмкость С наливаем 250мл из ёмкости А
Остаётся ёмкость В 1 литр перемешанного раствора, ёмкость А 250мл неразведенного равномерно, ёмкость С 250мл неразведенного равномерно.
Теперь из ёмкости В переливаем по 500 мл в ёмкость А и ёмкость С. Получается в ёмкости А 750мл равномерно разведенного раствора в ёмкости С 750мл равномерно разведенного раствора и ёмкость С пустая
1)3х+5=0,5х+10 - переносим все с Х в левую часть, а без Х в правую часть
3х-0,5=10-5 - складываем общие
2,5х=5 - находим Х
х=5/2,5
х=2
2)2,6+2х=1,9х+6,6 - переносим все с Х в левую часть, а без Х в правую часть
2х-1,9х=6,6-2,6 - складываем общие
0,1х=4 - находим Х
х=4/0,1
х=40
3)x+(х+1)+(х+2)=9 - раскрываем скобки
x+х+1+х+2=9 - переносим все с Х в левую часть, а без Х в правую часть
х+х+х=9-1-2 - складываем общие
3х=6 - находим Х
х=2
4)(z-2)+(z-1)+z=-3 - раскрываем скобки
z-2+z-1+z=-3 - переносим все с Х в левую часть, а без Х в правую часть
z+z+z=2+1-3 - складываем общие
3z=0 - находим Z
z=0
5)21+(20-4x)-(11-2x)=0 - раскрываем скобки
21+20-4x+11+2х=0 -переносим все с Х в левую часть, а без Х в правую часть
-4х+2х=-21-20-11 - складываем общие
-2х=-52 - находим Х
х=52/(-2)
х=-26
6)2u-3(7-2u)=3 - раскрываем скобки
2u-3*7+3*2u=3 -переносим все с Х в левую часть, а без Х в правую часть
2u+6u=3+3*7 - складываем общие
8u=3+21 - находим u
u=24/8
u=3
7)12-y=5(4-2y)+10 - раскрываем скобки
12-y=5*4-5*2y+10 -переносим все с Х в левую часть, а без Х в правую часть
-y+5*2y=10-12+5*4 - складываем общие
9y=18 - находим Y
y=18/9
y=2
8)2-2(x-8)=4x-4 - раскрываем скобки
2-2*x+2*8=4x-4 переносим все с Х в левую часть, а без Х в правую часть
-2х-4х=-2-4-2*8 - складываем общие
-6х=-22 - находим Х
х=(-22)/(-6)=22/6
х=3 целых 4/6 (дробь)