В решении.
Объяснение: По строкам:
| 2⁴ | 2 | 2⁴ | 2⁹
| 2³ | 2³ | 2³ | 2⁹
| 2² | 2⁵ | 2² | 2⁹
| 2⁹ | 2⁹ | 2⁹ (по столбцам)
1 диагональ - 2⁹;
2 диагональ - 2⁹.
Запись в тетради: 2*2*2*2 = 2⁴;
2*2*2 = 2³;
2*2 = 2²;
2*2*2*2*2 = 2⁵;
Первая строка: 2⁴*2*2⁴ = 2⁹;
Вторая строка: 2³*2³*2³ = 2⁹;
Третья строка: 2²*2⁵*2² = 2⁹;
Первый столбец: 2⁴*2³*2² = 2⁹;
Второй столбец: 2*2³*2⁵ = 2⁹;
Третий столбец: 2⁴*2³*2² = 2⁹.
Первая диагональ: 2⁴*2³*2² = 2⁹;
Вторая диагональ: 2⁴*2³*2² = 2⁹.
Вывод: в магическом квадрате сумма чисел в каждой строке, каждом столбце и на обеих диагоналях одинаковая.
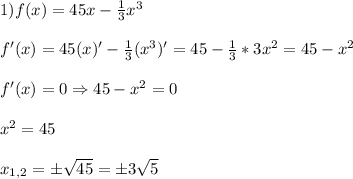
- + -
_____- 3√5______ 3√5 _____
min max
x = - 3√5 - точка минимума, так как при переходе через эту точку призводная меняет знак с "-" на "+" .
x = 3√5 - точка максимума, так как при переходе через эту точку призводная меняет знак с "+" на "-" .
2) f(x) = - 24x + x³
f'(x) = - 24(x)' + (x³)' = - 24 + 3x²
f'(x) = 0 ⇒ - 24 + 3x² = 0
x² = 8
x₁,₂ = ± √8 = ± 2√2
+ - +
______ - 2√2 ______ 2√2 ______
max min
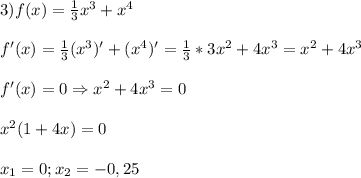
- + +
______ - 0,25 ____________0_____
min точка перегиба
4) f(x) = x³ - 15x⁴
f'(x) = (x³)' - 15(x⁴)'= 3x² - 15 * 4x³ = 3x² - 60x³ = 3x²(1 - 20x)
f'(x) = 0
3x² (1 - 20x) = 0
x₁ = 0
x₂ = 0,05
+ + -
______ 0,05 _______ 0 ______
точка перегиба max
Выносим 2 за скобку
Преобразуем числа в синус и косинус
В скобке - синус разности