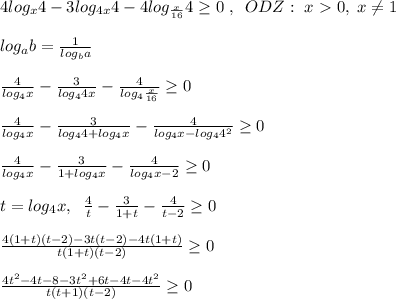
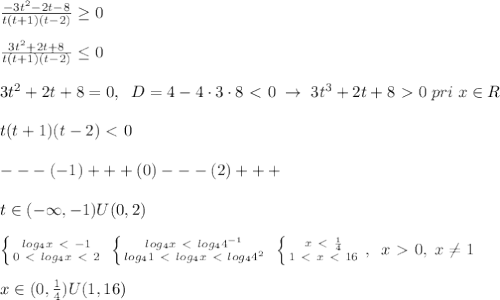
Найдем ОДЗ уравнения. Приравняем знаменатели дробей к нулю и решим уравнения. Их корни - это и есть ОДЗ. Записываем его:
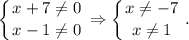 Основное свойство пропорции: произведение крайних членов пропорции равно произведению средних членов. То есть,
Основное свойство пропорции: произведение крайних членов пропорции равно произведению средних членов. То есть, 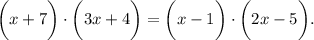 Раскрываем скобки по правилу "фонтанчика", собираем все в одну сторону уравнения, приводим подобные. Совершаем другие элементарные операции.
Раскрываем скобки по правилу "фонтанчика", собираем все в одну сторону уравнения, приводим подобные. Совершаем другие элементарные операции.
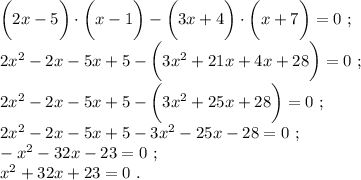
Забегу наперед и скажу, что фокус с теоремой Виета провернуть не получится. Применяем формулу дискриминанта и его корней. Запишем коэффициенты.
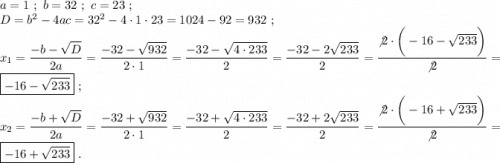
ответ: x₁=-16-√233; x₂=√233-16.
Для начала нужно разложить на множители знаменатель третьей дроби. Разложив, получим (х-5)*(х-4). Далее выберем общий множитель. Он будет таким: (х-3)(х-4)(х-5). Теперь сократим знаменатели дробей на данный множитель. У нас останется: х-5 + х-4 + х-3 ≤1. Перенесем числа -5, -4, -3 в другую часть неравенства, соответственно меняя знак на противоположный. Получится: х + х + х ≤ 1 + 5 + 4 + 3. Сложим числа и иксы:
3х ≤ 13. Разделим обе части на 3:
х ≤ четыре целых одна третья. Теперь осталось записать данное выражение в числовом промежутке: (-∞; четыре целых одна третья].
Решено.