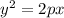 ее фокус находится в точке с координатами
ее фокус находится в точке с координатами 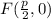
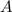 находиться в системе уравнения
находиться в системе уравнения 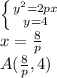 Если уравнение касательной равна
Если уравнение касательной равна 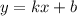 с учетом того что она проходит через точку
с учетом того что она проходит через точку 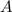 получаем
получаем 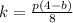 , подставляя
, подставляя 
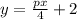
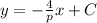 он проходит через точку
он проходит через точку 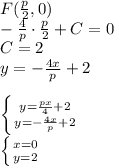
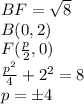
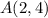
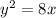
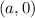 центр окружности (так как центр лежит на оси
центр окружности (так как центр лежит на оси 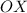 )
) 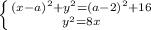
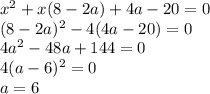
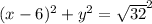
36.
Объяснение:
Пусть х - цифра из разряда десятков искомого двузначного числа,
у - цифра из разряда единиц, =>
(10х +у) - искомое двузначное число.
(х + у) - сумма цифр, => 4(х + у) = 10х + у ; (1)
(ху) - произведение цифр, => 2ху = 10х + у. (2)
Решим первое уравнение:
4(x + y) = 10x + y
4x + 4y = 10x + y
4y - y = 10x - 4x
3y = 6x
у = 2х
Подставим у = 2х во второе уравнение:
2х * 2х = 10х + 2х
4х² = 12х
4х = 12
х = 12 : 4
х = 3 - цифра из разряда десятков искомого двузначного числа.
у = 2 * 3 = 6 - цифра из разряда единиц.
36 - искомое двузначное число.
Проверка:
36 : (3 + 6) = 36 : 9 = 4
36 : (3 * 6) = 36 : 18 = 2
11(0,5х+1) + 23(0,5х-1) = 13х
5,5х+11+11,5х-23=13х
4х=12
х=3
Значит, время 3ч, а расстояние от А до В 3*13=39км
ответ: 39 км.