Для того, щоб подати дані вирази у вигляді стандартного многочлена, треба скористатися формулами скороченого множення:
а. (3-2х)(3+2х) + (2х-1)² ⇒ (a-b)(a+b) + 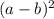 ⇒
⇒ 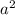 -
- 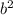 + a² - 2ab + b²;
+ a² - 2ab + b²;
(3-2х)(3+2х) + (2х-1)² = 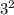 -
- 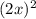 + (2x)² - 2×2x×1 + 1² = 9 - 4x² + 4x² - 4x +1 = 10 - 4x;
+ (2x)² - 2×2x×1 + 1² = 9 - 4x² + 4x² - 4x +1 = 10 - 4x;
б. (3-4у)(3+4у) ⇒ (a-b)(a+b);
(3-4у)(3+4у) = 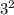 -
- 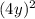 = 9 -
= 9 - 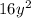 ;
;
в. (3-у)(9+3у+у²) ⇒ (a-b)(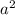 +ab+
+ab+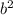 ) ⇒ a³- b³;
) ⇒ a³- b³;
(3-у)(9+3у+у²) = 3³- у³ = 27 - у³;
г. (2а-1)³ ⇒ (a-b)³ ⇒ a³ - 3a²b + 3ab² - b³;
(2а-1)³ = (2a)³ - 3×(2a)²×1 + 3×2a×1² - 1³ = 8a³ - 12a² + 6a - 1.
Для того, щоб подати дані вирази у вигляді стандартного многочлена, треба скористатися формулами скороченого множення:
а. (3-2х)(3+2х) + (2х-1)² ⇒ (a-b)(a+b) + 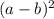 ⇒
⇒ 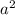 -
- 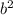 + a² - 2ab + b²;
+ a² - 2ab + b²;
(3-2х)(3+2х) + (2х-1)² = 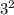 -
- 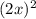 + (2x)² - 2×2x×1 + 1² = 9 - 4x² + 4x² - 4x +1 = 10 - 4x;
+ (2x)² - 2×2x×1 + 1² = 9 - 4x² + 4x² - 4x +1 = 10 - 4x;
б. (3-4у)(3+4у) ⇒ (a-b)(a+b);
(3-4у)(3+4у) = 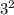 -
- 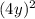 = 9 -
= 9 - 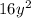 ;
;
в. (3-у)(9+3у+у²) ⇒ (a-b)(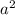 +ab+
+ab+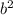 ) ⇒ a³- b³;
) ⇒ a³- b³;
(3-у)(9+3у+у²) = 3³- у³ = 27 - у³;
г. (2а-1)³ ⇒ (a-b)³ ⇒ a³ - 3a²b + 3ab² - b³;
(2а-1)³ = (2a)³ - 3×(2a)²×1 + 3×2a×1² - 1³ = 8a³ - 12a² + 6a - 1.
Косинус принимает свои значения на отрезке [-1;1], значит
Запишем в систему
Решаем отдельно
-1≤(a²+2a-2)/2
-2≤a²+2a-2
a²+2a≥0
a(a+2)≥0
a1 = 0
a2 = -2
___+__[-2]___-__[0]____+__
ответ этого неравенства x ∈ (-∞;-2] U [0;+∞)
(a²+2a-2)/2≤1
a²+2a-2≤2
a²+2a-4≤0
D=b²-4ac=4+16=20
a1 = -1-√5
a2 = -1+√5
__+_[-1-√5]___-__[-1+√5]___+__
ответ этого неравенства [-1-√5 ; -1+√5]
Объедененное решение: a ∈ [-1-√5 ; -2] U [0 ; -1+√5]
ответ: при a ∈ [-1-√5 ; -2] U [0 ; -1+√5] уравнение имеет решение