1) (1,75; 5,75)
2) (3; 3)
3) у = 7х
Объяснение:
Точкой пересечения графиков функций будет точка, (х,у), подходящая для обоих равенств.
То есть строго говоря это такая точка (х, у), где х и у являются решением системы уравнений:
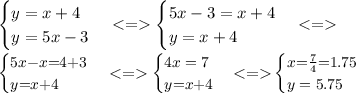
И искомые координаты точки будут (1,75; 5,75)
Можно решить проще:
Чтобы найти абсциссу (х) точки пересечения, приравняем

А ординату (у) точки пересечения найдем, подставив найденное значение (х) в любое из уравнений:
Например, в y = x + 4
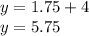
И искомые координаты точки будут (1,75; 5,75)
ответ (1,75; 5,75)
2.
Найти точку графика, абсцисса которой равна ординате

То есть требуется найти такую точку (х,у) графика,
у которой х = у.
Строго говоря, тут также требуется решение системы:
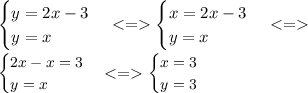
Это как бы пересечение двух графиков:
у = 2х - 3 и у = х
Но можно и проще.
Найти точку графика, абсцисса которой равна ординате, т.е. у = х.
Значит, подставляем х вместо у в уравнение;
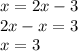
А так как по условию у = х, то

И искомые координаты точки будут (3; 3)
ответ: (3; 3)
3.
График линейной функции проходит через начало координат (т.е. точку О(0; 0)) и точку А(3; 21)
Следовательно, уравнение имеет форму
y = kx + b
причем т.к. график проходит через (0;0), следовательно
у(0) = 0 => 0 = k•0 + b <=> b = 0
а значит уравнение прямой имеет форму:
y = kx + 0 <=> y = kx
И т.к. график проходит через А(3; 21), следовательно
у(3) = 21 <=> k•3 = 21 <=> k = 21:3
k = 7
Итак, получили, что b = 0; k = 7
А значит уравнение примет вид:
у = 7х
ответ: у = 7х
Если Вы помните, рациональные числа были введены потому, что во множестве целых чисел не всегда можно выполнить деление. Например, существует целое число, которое является результатом деления 8 на 2, но не существует целого числа, которое является результатом деления 8 на 3. Поэтому были введены рациональные числа, то есть дроби вида p/q. Целые числа стали их подмножеством, когда q=1.
Для выполнимости деления рациональных чисел достаточно, но вот для извлечения корней - нет. Например, не существует рационального числа, которое было бы результатом извлечения квадратного корня из двух. (Это доказывается в Вашем учебнике, я уверен. Если не поняли, напишите, объясню.) Поэтому производят дальнейшее расширение системы чисел. К рациональным числам добавляют ещё и иррациональные, и все они вместе образуют множество действительных чисел.
Если не вдаваться в подробности, то рациональные числа можно отличить от иррациональных следующим образом. Рациональные числа, если их записать десятичной дробью, обязательно дадут конечную или бесконечную периодическую дробь. Это тоже легко доказать. Иррациональные же числа, записанные в виде десятичной дроби, оказываются представленными бесконечной НЕпериодической дробью.
Типичным примером иррационального числа является корень квадратный из двух. Пи - тоже иррациональное число, причем в определенном смысле более сложное, чем корень из двух, потому что Пи нельзя представить в виде корня из рационального числа. Но это уже немножко высший пилотаж