a) Вероятность взять один синий карандаш, равна 5/9. В коробке останется 8 карандашей. Вероятность взять второй синий карандаш, равна 4/8 = 1/2, вероятность взять третий сини карандаш равна 3/7. По теореме умножения, 5/9 * 1/2 * 3/7 = 5/42
Аналогично вероятность взять один красный карандаш равна 4/9, второй красный карандаш - 3/8, третий красный карандаш - 2/7. По теореме умножения, 4/9 * 3/8 * 2/7 = 1/21
По теореме сложения, вероятность взять 3 карандаша одинакового цвета равна 5/42 + 1/21 = 5/42 + 2/42 = 7/42 = 1/6
б) Всего всевозможных исходов: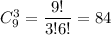 
из них нужно взять 2 синих и 1 красный карандаш, таких у нас 
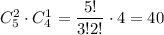. Вероятность того, что среди отобранных 3 карандаша 2 синих и 1 красный карандаш, равна 40/84 = 10/21
c) Вероятность того, что среди наугад выбранных 3 карандаша нет синего цвета, равна 1/21 (посчитали в пункте а), тогда вероятность того, что среди них будет хотя бы 1 карандаш синий, равна 1 - 1/21 = 20/21
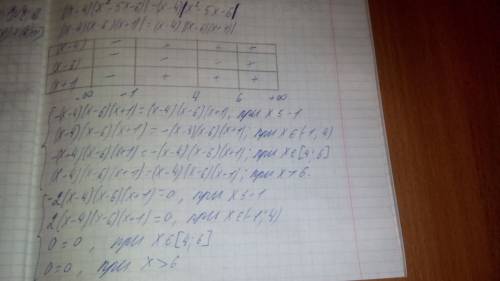
следующий вывод: x >= 4, т.к. модуль (по определению) число неотрицательное... следовательно, правая часть равенства должна быть >=0
и т.к. выражения кв.трехчленов абсолютно одинаковые, то любое
целое из промежутка [4; 15] будет решением...
это легко проверить: |(5-4)(25-25-6)| = 1*|25-25-6| ---> 6=6
или |(10-4)(100-50-6)| = 6*|100-50-6| ---> 6*44=6*44
нужно не забыть учесть корни кв.трехчлена --- по т.Виета это (-1) и (6)
6 ∈ [4; 15], следовательно, нужно еще включить (-1)
ответ: 13
((это числа -1,4,5,6,7,8,9,10,11,12,13,14,15)))