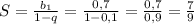
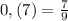
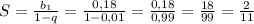
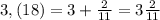
Для решения задачи воспользуемся теоремой о сумме углов выпуклого многоугольника.
Теорема : Для выпуклого n-угольника сумма углов равна 180°(n-2).
Значит, для нашего случая:
180(n-2)=3*80+x*150, где
3 угла по 80 градусов нам даны по условию задачи, а количество остальных углов нам пока неизвестно, значит обозначим их количество как x.
Однако, из записи в левой части мы определили количество углов многоугольника как n, поскольку из них величины трех углов мы знаем по условию задачи, то очевидно, что x=n-3.Таким образом уравнение будет выглядеть так:
180(n-2)=240+150(n-3)
Решаем полученное уравнение
180n - 360 = 240 + 150n - 450
180n - 150n = 240 + 360 - 450
30n = 150
n=5
Разложите на множители:
1)3t^2+7t+2
D = 49 - 4*3*2 = 25
t₁ = (- 7 - 5)/6
t₁ = - 2
t₂ = (- 7 + 5)/6
t₂ = - 1/2
3t^2+7t+2 = 3(t + 2)(t + 1/2)
2)p^3+8+6p^2+12p = (p + 2)³
Произвести действия, применив формулы сокращенного умножения:
1) (1+x^2)^2 = 1 + 2x² + x⁴
2) (2x+1)(2x-1) = 4x² - 1
3) (t-1)^3 = t³ - 3t² + 3t - 1
Выделить полный квадрат в трехчлене: x^ 2- 4x- 60 = (x² - 4x + 4) - 4 - 60 =
= (x - 2)² - 64
Решить пропорцию:2/7 = (2x+1)/9
2*9 = 7*(2x + 1)
18 = 14x + 7
14x = 11/14