Если f(- x) = f(x) , то функция чётная
Если f(- x) = - f(x) , то функция нечётная
1) f(x) = - 3x³ + 1
f (- x) = - 3 * (- x)³ + 1 = 3x³ + 1
f(x) ≠ f(- x) - значит функция не является чётной
- f(x) = - (- 3x³ + 1) = 3x³ - 1
f(- x) ≠ - f(x) - значит функция не является нечётной
ответ : f(x) = - 3x³ + 1 - не чётная и не нечётная
2) f(x) = 1/6 - 6x²
f(- x) = 1/6 - 6 * (-x)² = 1/6 - 6x²
f(x) = f(- x) - значит функция чётная
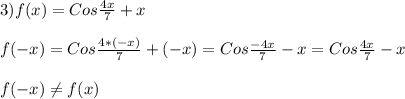
Значит функция не является чётной
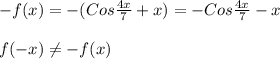
Значит функция не является нечётной
ответ : Функция не чётная и не нечётная
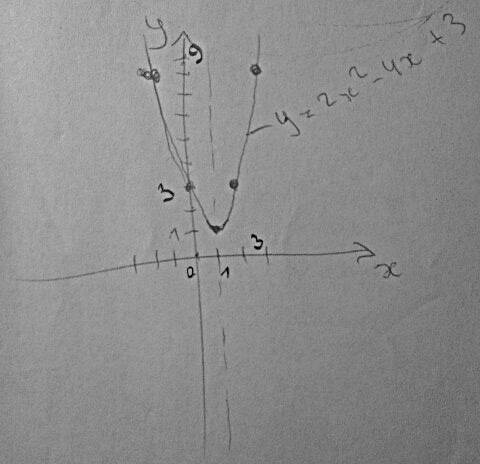
График - парабола,ветви вверх т.к коэфициэнт а - положительный.
Вершина:
x0= 4/4 = 1
y0=1
Таблица:
x I -1 I 0 I 1 I 2 I 3
y I 9 I 3 I 1 I 3 I 9
Строим график : ( см. рисунок)
Находим: 1) D = R
E= ( - бесконечность ; 1 ] U [ 1 ; + бесконечность)
2) точка пересеч. с Oy = (0;3)
3)f(x) возраст. при x принадлежащим к [ 1; + бесконечности).
f(x) убывает при x принадлежащим к (- бесконечность ; 1 ].
4) f(x)>0 при x принадлежащем множеству R.
f(x)<0 нет.
5) x max= нет x min = 1
y max = нет y min = 1
6) Функция является четной
7)= 5),по-моему...
* график я выполнила схемотически.
39+54=93 в обратном порядке 39
Если число записано двумя буквами х и у, то это двузначное число 10х+у
10х+у+54=10х+у+50+4=(10х+50)+(у+4)
Так как х+у=12, то у=12-х
(10х+50)+(у+4)=(10х+50)+(12-х+4)=10х+50+(16-х)=(10х+60)+(6-х)
получили число записанное в обратном порядке у десятков х единиц 10у+х
Приравниваем десятки и единицы
10х+60=10у
6-х=х ⇒2х=6 х=3
у=10·3+60=90
ответ.39