1. 1 ОДЗ х∈(-∞;+∞), т.к. дан многочлен.
2. с осью ох. у=0, х³-3х²+4=0, х=2, делим х³-3х²+4 на х-2, получаем
(х²-х-2)=(х+1)(х-2), чтобы разложить на множители, предварительно по теореме, обратной теореме Виета, угадали корни, это -1 и 2, итак, точек пересечения с осью ох найдено две (-1;0);(2;0). с осью оу х=0, тогда у=4, точка (0;4)
3. вертикальных нет, наклонные проверим к= предел при х, стремящемся к ∞ f(x)/x равен бесконечности, поэтому нет и наклонных асимптот.
4. y(-x)=-x³-3x²+4 ≠y(x) не является четной, y(-x)≠ -y(x) не является нечетной. это функция общего вида.
5.находим производную и точки экстремума и интервалы монотонности. у'=3х²-6х=0 зх*(х-2)=0; х=0;х=2, исследуя знак производной, получаем, что функция убывает на промежутке [0; 2] и возрастает на каждом из промежутков (-∞;0] и [2;+∞)
___02
+ - + точка х=0- точка максимума, х=2- точка минимума
6.находим вторую производную. 6х-6=0, точка х=1 точка перегиба, т.к. при переходе через нее вторая производная меняет знак с минуса на плюс. 1
- +
На промежутке (-∞;1) график функции выпуклый вверх, а на промежутке (1;+∞) вниз.
Функция не имеет промежутков убывания
Объяснение:
По теореме если угловой коэффициент прямой меньше нуля, то функция убывает, а если угловой коэффициент прямой больше нуля, то функция возрастает.
Докажем теорему
Рассмотрим функцию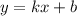 
.Где x,y - переменные; k,b - параметры. Продифференцируем функцию y.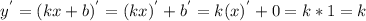
По теореме если производная больше нуля на промежутке M, то на этом промежутке функция возрастает.
По теореме если производная меньше нуля на промежутке M, то на этом промежутке функция убывает.
Тогда согласно теоремам:
если k < 0, то функция убывает.
если k > 0, то функция возрастает.
y=2x − 4 ⇒ k > 0, тогда функция возрастает при x є R.
б)(3,7^2+6,3*3,7)/111=(13.69+6.3*3.7)/111=73.963/111=0.6
в)(8,3^2-83*0.13)/0.7=(68.89-83*0.13)/0.7=-1.8343/0.7=2.6