
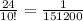

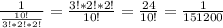
Для того чтобы решить эту задачу, нужно определить, за какое время девочки вымоют окна, работая вместе:
1) Обозначим производительность труда Маши за х, Лены – за у, а Насти – за с, а всю работу возьмем за 1.
2) Тогда время на выполнение всей работы Маши и Насти: х + с = 1/20.
3) Производительность труда Насти и Лены: у + с = 1/15.
4) Производительность труда Лены и Маши: х + у = 1/12.
5) Теперь сложим данные уравнения и найдем общую производительность труда: 2х + 2у + 2с = 1/5; 2 * (х + у + с) = 1/5; х + у + с = 1/10.
6) Тогда вместе девочки выполнят всю роботу за 10 минут.
Поэтому наш ответ: 10 минут.
При x∈(-3;5) производная отрицательная, значит функция убывает
При x∈(-бесконечность; -3) U (5; +бесконечность) - производная положительная, значит функция возрастает
На отрезке [0;6]:
x=-3 ∉ [0;6]
x=5 ∈ [0;6] - точка минимума
На отрезке [-2;2]:
x=-3 ∉ [-2;2]
x=5 ∉ [-2;2]