
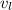 . Найдём скорость легкового автомобиля:
. Найдём скорость легкового автомобиля: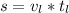
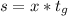
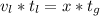
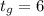 часов (2ч+4ч=6ч)
часов (2ч+4ч=6ч)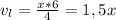 (км\ч).
(км\ч).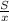 , а время, затраченное на прохождение всего пути, легковым автомобилем равно
, а время, затраченное на прохождение всего пути, легковым автомобилем равно 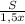 . Но т.к. легковой автомобиль потратил на дорогу на 1 час меньше времени чем грузовик, к тому же выехал на 2 часа позже, то можно записать следующее выражение:
. Но т.к. легковой автомобиль потратил на дорогу на 1 час меньше времени чем грузовик, к тому же выехал на 2 часа позже, то можно записать следующее выражение: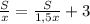
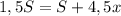
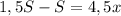
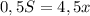
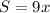
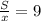 часов
часов