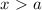X^4-2x^2-3 разложите на множители, если не трудно: 3

Question

Алгебра: X^4-2x^2-3 разложите на множители, если не трудно: 3

liakjv554211 · Accepted Answer

1. Число, определяющее положение точки на числовой оси, называется координатой точки на этой оси.

2. Множество чисел справа от точки a, отвечающих неравенству $x\ \textgreater \ a$ , называется открытым числовым лучом. Обозначается так: 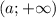$(a;+\infty)$ . Читается так: открытый числовой луч от a до плюс бесконечности.

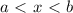3. Множество чисел, отвечающих условию $a\ \textless \ x\ \textless \ b$ называется интервалом. Обозначается так: (a,b)

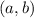. Читается так: интервал от a до b.

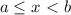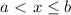4. Множества чисел, отвечающих условиям $a \leq x\ \textless \ b$ или $a\ \textless \ x \leq b$ , называются полуинтервалами. Множество 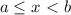$a \leq x\ \textless \ b$ обозначается так: [a;b)

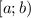, читается так: полуинтервал от a до b, включая a.

5. Числовые отрезки, интервалы, полуинтервалы и лучи называют числовыми промежутками.

MOGZ ответил