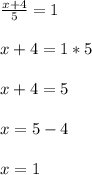
1) х₁=0, х₂=5, х₃=-5
2) х=1/12
3) х₁=3, х₂=4, х₃=-4.
Объяснение:
1) 4x³-100x = 0
Выносим общий множитель - 4х - за скобки.
4х(х²-25)=0
Произведение равно нулю тогда, когда хотя бы один из множителей равен нулю.
4х=0
х=0
х²-25=0
х²=25
х=±√25
х=±5
ответ: х₁=0, х₂=5, х₃=-5.
2) 144x^3-24x^2+x=0
Выносим общий множитель - х - за скобки.
х(144х²-24х+1)=0
х=0
144х²-24х+1=0
Квадратное уравнение решаем через дискриминант.
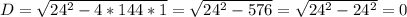
Уравнение будет иметь один корень, т.к. дискриминант равен нулю.
ответ: х=1/12.
3) x³-3x²-16x+48=0
Сгруппируем.
(х³-3х²)+(-16х+48)=0
Из первой скобки вынесем общий множитель х², а из второй (-16).
х²(х-3)-16(х-3)=0
Вынесем за скобки общий множитель (х-3).
(х-3)(х²-16)=0
х-3=0
х=3
х²-16=0
х²=16
х=±√16
х=±4
ответ: х₁=3, х₂=4, х₃=-4.
x ∈{-2} ∪ [2;7]
Объяснение:
1) Найдём нули функции у₁ = х²-5х-14:
х²-5х-14 = 0
х₁,₂ = 5/2 ± √(25/4 +14) = 5/2 ± √(81/4) = 5/2 ± 9/2
х₁ = 5/2 + 9/2 = 14/2 = 7
х₂ = 5/2 - 9/2 = - 4/2 = -2
Графиком функции у₁ = х²-5х-14 является парабола, ветви которой направлены вверх; следовательно, у₁ = х²-5х-14 ≤0 на участке
x ∈ [-2; 7].
2) Неравенство х² ≥ 4 эквивалентно неравенству: х²- 4 ≥ 0.
Найдём нули функции у₂ =х²- 4:
х²- 4 = 0
х² = 4
х = ± √4
х₃ = - 2
х₄ = 2
Графиком функции у₂ = х²- 4 является парабола, ветви которой направлены вверх; функция у₂ = х²- 4 больше или равна нулю на участках:
x ∈(-∞; -2] ∪ [2;+∞)
3) Объединяем полученные решения, для чего на числовой оси отмечаем точки х₂ = -2; х₃ = -2; х₄ = 2; х₁ = 7 и находим перекрываемые области значений, одновременно удовлетворяющие неравенству х²-5х-14 ≤ 0 и неравенству х² ≥ 4:
x ∈{-2} ∪ [2;7]
ответ: x ∈{-2} ∪ [2;7]