ответ: для первого - квадрат со стороной 12.
Объяснение:
1) P = 2a + 2b, S = ab. Докажем, что прямоугольник имеет наибольшую площадь, если он является квадратом.
Пусть одна из сторон прямоугольника равна х. Тогда вторая равна 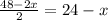 .
.
составим функцию: S(x) = x(24 - x) = 24x - x².
Найдем производную: S'(x) = 24 - 2x.
24 - 2х = 0; х = 12 - критическая точкаю
При переходе через точку х = 12 производная меняет знак с + на -. Следовательно, х - точка максимума, и в ней значение функции S(x) будет наибольшим.
Если а = 12 - первая сторона, то b = 24 - a = 12 - вторая сторона. Следовательно, искомый прямоугольник - квадрат со стороной 12 см.
В качестве опорной точки берём точку, лежащую в плоскости Oxy.
x + 2y = 7,
x + y = 5. Вычтем из первого уравнения второе: у = 2.
х = 5 - у = 5 - 2 = 3.
Получили точку (3; 2; 0).
Теперь найдём направляющий вектор прямой как векторное произведение нормальных векторов плоскостей.
i j k | i j
1 2 4 | 1 2
1 1 1 | 1 1 = 2i + 4j + 1k - 1j - 4i - 2k = -2i + 3j - 1k.
Нашли направляющий вектор (-2; 3; -1).
Получаем ответ - уравнение прямой по точке и направляющему вектору: (x - 3)/(-2) = (y - 2)/3 = z/(-1).
Приравняв эти дроби параметру t, получим параметрические уравнения прямой:
x = -2t + 3,
y = 3t + 2,
z = -t.