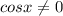sin²x - cosx · sinx = 0,
sinx(sinx - cosx) = 0,
sinx = 0 или sinx - cosx = 0
x = πn, n ∈ Z sinx = cosx, | : cosx ≠0,
tgx = 1,
x = π/4 + πk, k ∈ Z
ответ: πn, n ∈ Z; x = π/4 + πk, k ∈ Z.
2. sin2a=(sina+cosa)^2-1
Преобразуем левую часть, по формуле синуса двойного угла получим: 2sinacosa
Преобразуем правую часть. Возведем в квадрат, получим: sin^2a+2sinacosa+cos^2a-1
Далее представим 1 как cos^2a+sin^2a (основное тригонометрическое тождество), получим: sin^2a+2sinacosa+cos^2a-cos^2a-sin^2a=2sinacosa
Левая и правая часть равны. Что и требовалось доказать.
3.Разложим cos2a=cos^2a-sin^2a
Найдем cos^2a по основному тригонометрическому тождеству, он равен 1-sin^2a=1-9/25=16/25
Ну теперь найдем то, что надо найти :)
cos2a=16/25-9/25=7/25=0,28
1. ctg240=ctg(270-30)=tg30=корень из трех на три
cos7pi/3= cos(2pi+pi/3)=cospi/3=1/2
sin1560=sin(1530+30)=cos30=1/2
Вот и все решение :)
n-целое
поделим на