Таких точек 2 - одна точка касания, вторая - точка пересечения.
Находим точку касания.
y(k) = y'(хо)*(x - xo) + y(xo).
Производная равна y' = x² - 4.
Подставим координаты точки М, через которую проходит касательная.
18 = (xо² - 4)*(0 - хо) + (1/3)хо³ - 4хо,
-xо³ + (1/3)хо³ = 18,
(-2/3)хо³ = 18,
хо³ = -54/2 = -27.
хо = ∛(-27) = -3.
уо = (1/3)*(-27) - 4*(-3) = -9 + 12 = 3.
Точка касания А(-3; 3).
Уравнение касательной:
y(k) = (9 - 4)*(x -(-3) + (-9 + 12) = 5x + 15 + 3 = 5x + 18.
Находим точку пересечения.
5x + 18 = (1/3)x³ - 4x,
(1/3)x³ - 9x - 18 = 0.
Разложив на множители (х - 6)(х + 3)² = 0 получаем 2 корня:
х = 6 и х = -3 (это точка касания).
Точка В: у = 5*6 + 18 = 48.
ответ: точки А(-3; 3) и В(6; 48).
1. Чтобы записать уравнение окружности, не хватает радиуса.
Стоит отметить, что расстояние от центра окружности до прямой x=3 равно радиусу, так как окружность касается этой прямой.
Центр имеет абсциссу, равную -1, а прямая -- равную 3
Найдём расстояние между -1 и 3:
R = |-1| + |3| = 1 + 3 = 4 -- радиус окружности
Теперь запишем уравнение окружности:
(x - x₀)² + (y - y₀)² = R², где (x₀, y₀) -- координаты центра окружности, R -- её радиус
(x + 1)² + (y - 5) = 16
2. Чтобы функция была чётная, нужно выполнение равенства:
y(x) = y(-x)
y(x) = xⁿ * xⁿ⁻² - 4
y(-x) = (-x)ⁿ * (-x)ⁿ⁻² - 4 = (-1 * x)ⁿ * (-1 * x)ⁿ⁻² - 4 = (-1)ⁿ * xⁿ * (-1)ⁿ⁻² * xⁿ⁻² - 4 = (-1)ⁿ⁺ⁿ⁻² * xⁿ * xⁿ⁻² - 4 = (-1)²⁽ⁿ⁻¹⁾ * xⁿ * xⁿ⁻² - 4 = 1ⁿ⁻¹ * xⁿ * xⁿ⁻² - 4 = xⁿ * xⁿ⁻² - 4
Итого y(x) = y(-x), следовательно функция чётная
3. Сначала отдельно рассмотрим первый корень. Рассмотрим подкоренное выражение, соберём из него квадрат суммы (a+b)² = a² + 2ab + b²:
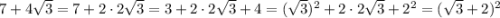
Тогда выражение примет вид:
![\sqrt[10]{7+4\sqrt{3}} \cdot\sqrt[5]{\sqrt{3}-2}= \sqrt[10]{(\sqrt{3}+2)^2} \cdot\sqrt[5]{\sqrt{3}-2}= \sqrt[5]{\sqrt{3}+2} \cdot\sqrt[5]{\sqrt{3}-2}= \sqrt[5]{(\sqrt{3}+2)(\sqrt{3}-2)} =\sqrt[5]{(3-4)}=\sqrt[5]{-1}=-1](/tpl/images/0970/8390/45093.png)
ответ: a=-25/36
Объяснение:
Исключим переменную z из системы уравнений.
Для этого умножим первое уравнение на (-3) :
-3x-3y-3z=-6x^2-9y^2
-x+2y+3z=a
Cложим уравнение 1 и 2:
-4x-y= a-6x^2-9y^2
6x^2-4x +9y^2-y=a
(√6x- √6/3)^2 +(3y-1/6)^2= a+2/3 +1/36= a + 25/36
(√6x- √6/3)^2 +(3y-1/6)^2=a+25/36
Когда : a+25/36 <0 решений нет , поскольку сумма двух квадратов число неотрицательное.
Когда : a+25/36=0 → a=-25/36
(√6x- √6/3)^2 +(3y-1/6)^2=0
В этом случае уравнение имеет единственное решение в силу того что квадраты неотрицательны.
√6x- √6/3=0
x=1/3
3y-1/6=0
y=1/18
z можно вычислить используя уравнение 2.
Если a+25/36>0
Значение x будет зависит от значения y.
Решение будет существовать при таких y когда:
(a+25/36)>(3y-1/6)^2
Таким образом решением данного уравнения будет совокупость двух отрезков, то есть решений будет больше чем одно.
Вывод: cистема уравнений имеет единственное решение , только когда a=-25/36