1)найти сумму корней уравнения: х^3-3х^2-4х +12=0 (представьте само решение ,) 2) при каком значении - id417286820221003 от помощь155 03.10.2022 00:53

Question

Алгебра: 1)найти сумму корней уравнения: х^3-3х^2-4х +12=0 (представьте само решение ,) 2) при каком значении параметра а уравнение ах^2-х+3=0 имеет 1 корень

помощь155 · Accepted Answer

3 насоса наполняют 2-й танкер за 40 часов.

Объяснение:

Исправим условие задачи.

"Четыре одинаковых насоса, работая вместе, наполнили нефтью первый танкер и ЧЕТВЕРТЬ второго, другого объема, за 11часов. Если бы три насоса наполнили первый танкер, а затем ТРЕТЬ второго, то работа заняла бы 18часов. За сколько часов три насоса могут наполнить второй танкер?"

Пусть х - время, за которое 1 насос наполняет танкер А

у - время за которое 1 насос наполняет танкер В.

По 1-му условию:

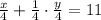
$\frac{x}{4} + \frac{1}{4} \cdot \frac{y}{4} =11$

или

4х + у = 176 (1)

По 2-му условию:

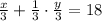
$\frac{x}{3} + \frac{1}{3} \cdot \frac{y}{3} =18$

или

3х + у = 162 (2)

Вычтем из уравнения (1) уравнение (2)

х = 179 - 162

х = 14

Из уравнения (1) получим

у = 176 - 4х = 176 - 4 · 14 = 120

Один насос наполняет танкер В за 120 часов, тогда три насоса делают это в 3 раза быстрее, то есть за 40 часов

120ч : 3 = 40 ч

1)найти сумму корней уравнения: х^3-3х^2-4х +12=0 (представьте само решение ,) 2) при каком значении параметра а уравнение ах^2-х+3=0 имеет 1 корень

MOGZ ответил