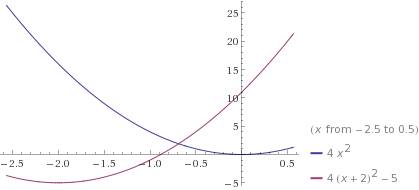
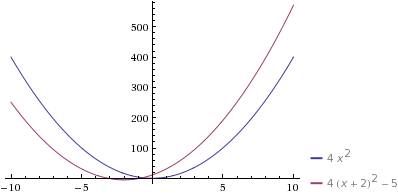
если для первого графика y = 4x^2 вершина находится в точке (0;0), то
ось симметрии параболы - ось OY (уравнение x=0)
то для второго графика ось симметрии сместится влево на 2 (уравнение x = -2, все первое слагаемое обратится в 0 и получится y = -5), т.е. для второго графика вершина опустится вниз по оси OY на 5 единиц и сместится влево на 2 единицы по оси OX
координаты вершины новой параболы (-2;-5), ветви вверх и она в точности повторяет первый график (из новой точки---новой вершины), иными словами
новый график получится параллельным переносом исходного графика вниз по оси OY на 5 единиц и влево по оси OX на 2 единицы
x-5<=0; x<=5;
x∈[4;5]
ответ: x∈[4;5]
2) х(х-41)>0; x>0
x-41>0; x>41
x∈(-∞, 0)⋃(41, +∞)
ответ: x∈(-∞, 0)⋃(41, ∞)
3) x^2-25<0; (x-5)(x+5)<0;
x<5 ; x<-5
x∈(-5, 5)
ответ: x∈(-5, 5)
4) (x^2-36)/x>=0
ОДЗ x>=0 ; x∈[0, +∞);
(x-6)(x+6)>=0;
x∈(-∞, -6]⋃[6, +∞)
x∈[-6, 0)⋃[6, +∞) - c учетом ОДЗ
ответ: x∈[-6, 0)⋃[6, +∞)
5) -x^2+25x<0 |*(-1);
x^2-25x>0;
x(x-25)>0
x>0; x-25>0; x>25
x∈(-∞, 0)⋃(25, +∞)
ответ: x∈(-∞, 0)⋃(25, ∞)
6) (x^2-7x+10)/(x-4)>=0;
ОДЗ: x-4>=0; x>=4 ; x∈[4, +∞);
(x^2-7x+10)>=0
По т. Виета:
x∈(-∞, 2]⋃[5, +∞);
x∈[2, 4)⋃[5, ∞) - c учетом ОДЗ;
ответ: x∈[2, 4)⋃[5, ∞)