ответ:1)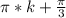
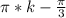
2) НЕТ ДЕЙСТВИТЕЛЬНЫХ РЕШЕНИЙ
Второе даже решать не буду там и так ясно что нет решений а первое вот:
1)разложи косинус получишь
4 sin^4 x = 5-5*sin^2(x) + 1
2)заменяем sin^2 x=t
-1<t<1
4*t^2=5-5*t+1
4*t^2+5t-6=0
t=-2 t=3/4 (по т.виета)
||
\/
sin^2 x=-2 sin^2 x = 3/4
нет решений
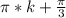
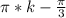
т.к. sinx=корень из 3/ 2
тк -1<sinx<1 x=arcsin( корень из 3/ 2)+pi*k
x=-arcsin( корень из 3/ 2)+pi*k
arcsin( корень из 3/ 2)=pi/3
отсуда
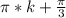
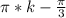
Пусть боковая сторона равнобедренного треугольника - х см, тогда основание треугольника будет 18-2х или 2(9-х) см.
Составим выражение для высоты треугольника, проведенной к основанию
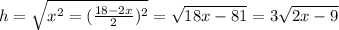
Теперь составим выражение площади треугольника

Найдем производную полученного выражения

при x<6 значение производной S'>0, а при x>6 S'<0, значит при х=6 функция S принимает максимальное значение (максимум функции)
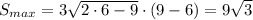
Таким образом, плащадь треугольника будет наибольшей, если все его стороны будут равны 6 см, т.е. он будет равносторонним.
a) ΔABK, он прямоугольный. в нём АВ = 9 и АК = 9/2
По т. Пифагора ищем ВК
ВК²= 9² - (9/2)² = 81 - 81/4 = 81·3/4
ВК = 9√3/2
ВО = 2/3 ВК = 2/3· √3/2 = 3√3
б) ΔSBO прямоугольный. По т. Пифагора ищем ВO = H
BO² = 14² - (3√3)² = 196- 27 = 169
ВО =13