Уравнение квадратной параболы в общем виде: у = ах² + вх + с Найдём коэффициенты а, в, с Подставим координаты точки А -6 = а· 0² + в·0 + с → с = -6 Подставим координаты точки В -9 = а·1² + в·1 - 6 → а + в = -3 (1) Подставим координаты точки С 6 = а·6² + в·6 - 6 → 6а + в = 2 → в = 2 - 6а (2) Подставим (2) а (1) а + 2 - 6а = -3 → а = 1 Из (2) получим в = -4 Итак, мы получили уравнение параболы: у = х² - 4х - 6 Абсцисса вершины параболы: m =-в/2а = 4 / 2 = 2 Ординату вершины параболы найдём, подставив в уравнение параболы х = m = 2 у = 2² - 4 · 2 - 6 = -10 ответ: вершиной параболы является точка с координатами (2; -10)
X - скорость катера в стоячей воде y - скорость течения реки или скорость плота x+y - скорость катера по течению x-y - скорость катера против течения 90/(x+y) - время катера на путь по течению 90/(x-y) - время катера на путь против течения 30/y - время плота до встречи 90/(x+y)+60/(x-y) - время катера до встречи Имеем систему 90/(x+y)+90/(x-y)=12,5 90/(x+y)+60/(x-y)=30/y или первое уравнение оставляем и приводим к общему знаменателю, а второе уравнение получаем вычитанием второго из первого. Новая система: 90(x-y+x+y)=12,5(x-y)(x+y) 30/(x-y)=12,5-30/y или 30/(x-y)+30/y=12,5; 30(y+x-y)=12,5y(x-y)
180x=12,5(x-y)(x+y) 30x=12,5y(x-y) Делим первое уравнение на 2-ое: 6=(x+y)/y⇒6y=x+y⇒x=5y подставляем во 2-е уравнение вместо x его значение 5y: 30*5y=12,5y(5y-y)⇒4y*12,5=150; 50y=150⇒y=3; x=15 Скорость катера в стоячей воде - 15 скорость течения - 3
1)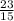 км\мин- скорость мотоциклиста
км\мин- скорость мотоциклиста
2)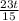 км - проедет мотоциклист за t мин., если будет ехать с той же скоростью
км - проедет мотоциклист за t мин., если будет ехать с той же скоростью
ответ: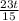 км
км