Функции отличается от при x>0 тем, что она быстрее убывает. Функция - чётная т.к. степень при единственном "x" чётная.
y=2x - функция прямой пропорциональности (y=kx), её график будет в 3 и 1 четверти (k>0), поэтому пересечении с может быть только в 1 четверти. Такое же и с прямой x=4.
Найдём абсциссу точки пересечения функций и y=2x.
Абсцисса точки пересечения графиков функций , x=4 и y=2x, x=4 уже известна (x=4).
1. В сентябре 30 дней. Дни которые кратны 5: 5;10;15;20;25;30 - всего 6 Всего благоприятных событий: 6. Всего все возможных событий: 30. Искомая вероятность :
2. Вероятность того, что на монете выпала решка равна 1/2, а вероятность того, что на игральной кости выпало нечетное число очков равно 3/6=1/2. Поскольку событий независимы, то вероятность того, что выпали на монете решка, а на кости нечетное число очков равна 1/2 * 1/2 = 1/4.
3. Найдем вероятность того, что карта король черной масти: Всего все возможных событий: . Всего благоприятных событий: Тогда вероятность
4. Всего все возможных событий: 36 сумма выпавших число очков не больше 3: {1;2}, {2;1}, {1;1}- всего 3 (благоприятных событий) Вероятность того, что сумма выпавших число очков не больше 3 равна
Тогда вероятность того, что сумма выпавших число очков не меньше 3 равна
5. Всего все возможных событий: . Взять 2 красных шаров можно
1. В сентябре 30 дней. Дни которые кратны 5: 5;10;15;20;25;30 - всего 6 Всего благоприятных событий: 6. Всего все возможных событий: 30. Искомая вероятность :
2. Вероятность того, что на монете выпала решка равна 1/2, а вероятность того, что на игральной кости выпало нечетное число очков равно 3/6=1/2. Поскольку событий независимы, то вероятность того, что выпали на монете решка, а на кости нечетное число очков равна 1/2 * 1/2 = 1/4.
3. Найдем вероятность того, что карта король черной масти: Всего все возможных событий: . Всего благоприятных событий: Тогда вероятность
Тогда вероятность того, что карта не король черной масти:
4. Всего все возможных событий: 36 сумма выпавших число очков не больше 3: {1;2}, {2;1}, {1;1}- всего 3 (благоприятных событий) Вероятность того, что сумма выпавших число очков не больше 3 равна
Тогда вероятность того, что сумма выпавших число очков не меньше 3 равна
5. Всего все возможных событий: . Взять 2 красных шаров можно
Функции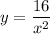 отличается от
отличается от 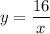 при x>0 тем, что она быстрее убывает. Функция
при x>0 тем, что она быстрее убывает. Функция 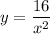 - чётная т.к. степень при единственном "x" чётная.
- чётная т.к. степень при единственном "x" чётная.
y=2x - функция прямой пропорциональности (y=kx), её график будет в 3 и 1 четверти (k>0), поэтому пересечении с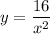 может быть только в 1 четверти. Такое же и с прямой x=4.
может быть только в 1 четверти. Такое же и с прямой x=4.
Найдём абсциссу точки пересечения функций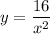 и y=2x.
и y=2x.
Абсцисса точки пересечения графиков функций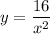 , x=4 и y=2x, x=4 уже известна (x=4).
, x=4 и y=2x, x=4 уже известна (x=4).
Схематичный график смотри внизу.
Получается, что
ответ: 8.