Случай 1. Пусть первый будет лжецом, а второй - рыцарем. Правдолюб сказал, что на острове 1002 Л и 1002 Р , потому что 1001 Р + он сам.
Лжец же сказал, что на острове 1004 Лжеца, вместе с ним и 1004 Р. Т.е. он соврал дважды, прибавив по 2 человека к Лжецапм и правдолюбам. Значит на острове 1002 Л и 1002 Р
Случай 2. Пусть теперь первый будет Р, а второй Л. Рыцарь сказал, что на острове 1003 лжеца и 1005 Рыцарей вместе с ним. Лжец утверждает, что на острове 1003 лжецы и 1001 рыцарь. Очевидно, что как бы мы не прибавляли и не убавляли 2, нужного ответа у нас не получится.Значит, верный ответ только один.
ответ: На острове 1002 лжеца и 1002 рыцаря
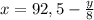, так как искомое число является целым, очевидно, чтоб его получить нужно от 92,5 отнять 0,5, исходя из дроби 
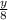и ряда слагаемых к первому числу (+1; +2; +3 ... +6) это +4, то есть 
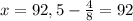- первое по счету число, соответственно седьмое 92+6=98
x+y =1
x⁴ +y⁴ =17
Симметричные уравнения
* * * Известно : (x+y)⁴ =x⁴ +4x³y +6x²y² +4xy²+y⁴ * * *
{x+y =1; (x+y)⁴ -4x³y -4xy³ -6x²y² =17.
{x+y =1;(x+y)⁴ -4xy(x²+y²) -6x²y² =17 .
{x+y =1;(x+y)⁴ -4xy ((x+y)² -2xy ) -6(xy)² =17 .
{x + y =1 ; 1 -4xy(1- 2xy) -6(xy)² =17 .
1 -4xy(1- 2xy) -6(xy)² =17 .
1 -4xy+8(xy)² -6(xy)² =17 .
2(xy)² - 4xy -16 =0 .
(xy)² - 2xy -8 =0 .
(xy)₁ = - 2;
(xy)₂ = 4 ;
a) { x+y =1; xy = -2 ⇔t² -t -2 =0 * * * x² -x -2 =0 или y² -y -2 =0 * * *
t₁ = -1 ;t₂ =2.
x₁ = -1 ; y₁ =2 или x₂ =2 ; y₂ = -1 .
(-1; 2) или (2 ;-1)
б) { x+y =1; xy =4=0 ⇔t² -t +4 =0 не имеет решения .
ответ : (-1; 2) , (2 ;-1)