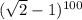 раскрыть 100-ую степень по биному Ньютона, то получится сумма слагаемых вида
раскрыть 100-ую степень по биному Ньютона, то получится сумма слагаемых вида 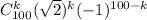 по k от 0 до 100. При четных k эти слагаемые будут натуральными числами, а при нечетных k они имеют вид
по k от 0 до 100. При четных k эти слагаемые будут натуральными числами, а при нечетных k они имеют вид 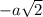 , где а - натуральное. Значит,
, где а - натуральное. Значит, 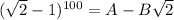 , при некоторых натуральных
, при некоторых натуральных 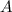 и
и 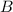 . (для решения задачи нет нужды их явно вычислять). Опять же из бинома Ньютона понятно, что тогда
. (для решения задачи нет нужды их явно вычислять). Опять же из бинома Ньютона понятно, что тогда 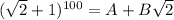 , т.к. в нем будут те же слагаемые, только все со знаком плюс. Перемножив эти два соотношения, получим
, т.к. в нем будут те же слагаемые, только все со знаком плюс. Перемножив эти два соотношения, получим 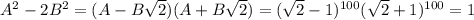 , то есть
, то есть 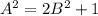 . Поэтому, если положим
. Поэтому, если положим 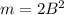 , то получим, что
, то получим, что 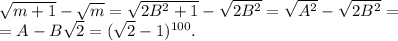
Уравнение здесь имеет вид u3+u=v3+v, где u=2x2, v=3x+5a. От него можно перейти к равносильному равенству u=v по следующей причине. Функция f(u)=u3+u имеет производную f′(u)=3u2+1, которая всюду положительна. Поэтому f(u) строго монотонно возрастает на всей области определения. Поэтому её значения в различных точках не могут совпадать. Таким образом, мы приходим к равносильному условию u=v, а это квадратное уравнение 2x2−3x−5a=0. Находим дискриминант, и пишем, что он положителен: в этом и только в этом случае уравнение будет иметь более одного корня.