Переформулируем условие в терминах арифметической прогрессии:
1) В первый день потратили 100 рублей = первый член прогрессии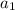 
равен 100.
2) Каждый последующий день тратили на 50 рублей больше = разность прогрессии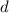 
равна 50.
3) Всего было 1000 рублей = сумма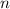 
членов (то есть 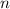дней) равна 1000.
Сумма вычисляется по формуле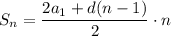 
Чтобы найти 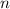, подставим в эту формулу известные числа:
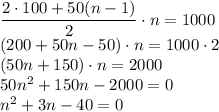
Решим это уравнение с дискриминанта:
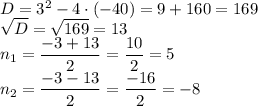
Количество дней не может быть отрицательным, поэтому имеем единственный ответ: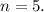 
ответ: на пять дней.
Здесь надо учесть четыре ограничения:
1) Подкоренное выражение не должно быть отрицательным:
![x^2-4^2\geqslant 0\\(x-4)(x+4) \geqslant 0\\x \in (- \infty; -4] \cup [4; + \infty)](/tpl/images/3214/7548/cb21f.png)
2) Выражение под логарифмом должно быть положительным: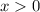 
3) Знаменатель первой дроби должен быть ненулевым
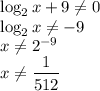
4) Знаменатель второй дроби также должен быть ненулевым:
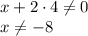
Теперь объединим эти промежутки (лучше сделайте это на листке бумаги, чтобы видеть наглядно): по второму условию икс положителен, поэтому первое условие сокращается до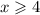 
Третье условие не удовлетворяет предыдущему, поэтому вычёркивается.
Четвёртое условие также вычёркивается как отрицательное.
ответ: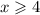
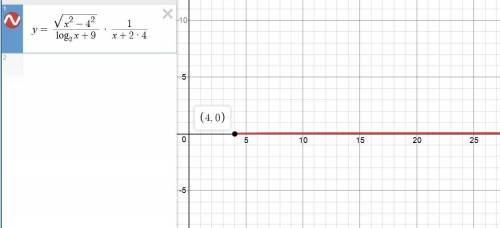
Вот так выглядит график этой функции, построенный на компьютере (см. скриншот).
P. S. Если появились какие-либо вопросы, задавайте.
8n + 1 = km, где k ∈ N
Если число 5n + 2 делится на m, то его можно представить в виде:
5n + 2 = tm, где t ∈ N
Получилось два равенства:
8n + 1 = km (1)
5n + 2 = tm (2)
Как при решении систем уравнений методом сложения выполним следующее: первое умножим на 5, второе умножим на 8:
40n + 5 = 5km
40n + 16 = 8tm
Теперь вычтем из одного равенства второе:
40n + 5 - (40n + 16) = 5km - 8tm
5 - 16 = 5km - 8tm
8tm - 5km = 11
m(8t - 5k) = 11
Произведение двух чисел m и (8t - 5k) равно 11. Но число 11 - простое.
Его в виде произведения можно представить только единственным
11 · 1
m(8t - 5k) = 11 · 1
Тогда или m = 1, или m = 11.
В условии сказано, что число m ≠ 1, тогда m = 11.
ответ: m = 11.