Надо приравнять log2(х) = 5 - log2(x+14).
log2(х) + log2(x+14) = 5.
Сумма логарифмов равна логарифму произведения, а цифру 5 представим так: 5 = log2(32).
log2(х*(x+14)) = log2(32).
При равных основаниях логарифмирумые выражения равны.
х*(x+14) = 32. Раскроем скобки:
х² + 14х - 32 = 0.
Квадратное уравнение, решаем относительно x:
Ищем дискриминант:
D=14^2-4*1*(-32)=196-4*(-32)=196-(-4*32)=196-(-128)=196+128=324;
Дискриминант больше 0, уравнение имеет 2 корня:
x_1=(√324-14)/(2*1)=(18-14)/2=4/2=2;
x_2=(-√324-14)/(2*1)=(-18-14)/2=-32/2=-16 - не принимаем по ОДЗ.
По значению абсциссы х = 2 находим ординату:
y=log2(2) = 1.
1 число - х
2 число - у
система ур-ий
х+у=14
ху=36,75
выражаем из 1 ур-ия х
х=14-у
подставляем во 2 ур-ие
(14-у)*у=36,75
14у-у^2-36.75=0
y^2-14у+36,75=0
решаем квадратно ур-ие
D=(-14)^2-4*1*36.75=196-147=49
х1=(-(-14)+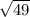 )/2*1=(14+7)/2=21/2=10,5
)/2*1=(14+7)/2=21/2=10,5
х2=(-(-14)-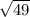 )/2*1=(14-7)/2=7/2=3,5
)/2*1=(14-7)/2=7/2=3,5
корни уравнеия (10,5 и 3,5)
х=10,5
тогда у=14-10,5=3,5
х=3,5
тогда у = 14-3,5=10,5