Законы сложения и умножения:
4+5=5+4, потому что и так и так равно 9(от перемены мест слагаемых сумма не меняется)
3*9=9*3(от произведений множителей произведение не меняется, будет 27)
(7+3)+8=8+(7+3) тут вообще что хочешь выноси, если раскроешь скобки 7+3+8=18 тут правило раскрытия скобок.
(7*5)*4=4*(7*5) тут ничего не поменяется(если ты сделаешь, допустим, (4*5)*7 будет одно и тоже, тут правило раскрытие скобок именно в случае в скобках)
6(4+5)=6*4+6*5 тут ты просто умножаешь число перед скобкаии на все цифры в скобках и ставишь знаки без изменениний(не считая если перед скобкаии отрицательное число)
Правила раскрытия скобок:
6+(21+9)=6+21+9 по моему тут всё понятно
6+(21-7)=6+21-7
9-(6+2)=9-6-2(туь будет тоже самое что сначала сложить в скобках и вычесть, т. Е. Ты складываешь 6+2 и будет 8, 9-8=1,если от 9 отнимешь все поочерёдно, то тоже будет 1)
9-(2-1)=9-2+1
1) a) 2x²-8;
недопустимых значений переменной x не существует, т.к 2x²-8 - не знаменатель дроби, нет корня и т.д => x ∈ R
б) дробь имеет смысл, когда знаменатель не равен нулю: x-2≠0
x≠2
x∈(-∞; 2) ∪ (2; +∞)
в) x+3≠0
x≠-3
x ∈ (-∞; -3) ∪ (-3; +∞)
2) a) дробь имеет смысл, когда знаменатель не равен нулю
y²-4≠0
(y-2)(y+2)≠0
y≠-2
y≠2
y ∈ (-∞; -2) ∪ (-2; 2) ∪ (2; +∞)
б) дробь имеет смысл, когда знаменатель не равен нулю
y²+1≠0
y²≠-1 - нет действительных корней
y∈R
в) дроби имеют смысл, когда знаменатели не равны нулю
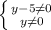
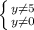
y ∈ (-∞; 0) ∪ (0; 5) ∪ (5; +∞)
Объяснение:
3m-2n будет минимально при минимальном m и при максимальном n
т.е. m=3, n=5 3m-2n=9-10
3m-2n будет максимально при m максимальном и n минимальном
т.е. m=6 n=4
3m-2n=18-8=10
ответ: -10<(3m-2n)<10
2)
m/n в данном случае будет минимально при минимальном m и при максимальном n
m=3, n=5
(m/n)=3/5
m/n в данном случае будет максимально при m максимальном и n минимальном
m=6, n=4
(m/n)=3/2
ответ: 3/5<(m/n)<3/2