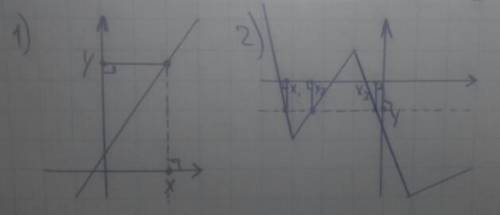
1)
Дана абсцисса точки.
Найти ординату точки графика функции, с данной абсциссой.
На оси абсцисс из данной абсциссы проводим перпендикуляр к оси абс. Из точки, пересечения перпендикуляра с графиком функции, проводим перпедикуляр к оси ординат. Точка имеет ту же ординату, что и точка пересечения перпендикуляра с осью орд.
2)
Дана ордината точки.
Найти абсциссу точки(ек) графика функции, с данной ординатой.
На оси ординат из данной орд. проводим перпендикуляр к оси орд. Из точек, пересечения перпендикуляра с графиком функции, проводим перпедикуляры к оси абс. Точки имеют абсциссу, соответствующую точки пересечения перпендикуляра с осью абс.
=5cosβ- 4sin(3π/2 -β) =|| формула приведения: sin(3π/2 -β)= -cosβ ||= 5cosβ- 4 (-cosβ) =5cosβ+4osβ =9cosβ = 9(-1/3) = -3.