а) Преобразуйте выражение, чтобы получить многочлен стандартного вида. Укажите степень многочлена.
(2х² - 2)² - 4х³(х³ + х² - х - 2) + 4(х²)³ + 20х⁹/5х⁴ - 2(4х³ + 1) =
= 4х⁴ - 8х² + 4 - 4х⁶ - 4х⁵ + 4х⁴ + 8х³ + 4х⁶ + 4х⁵ - 8х³ - 2 =
= 8х⁴ - 8х² + 2. Стандартный вид. Степень (х⁴) = 4.
б) Докажите, что при любых целых значениях x многочлен делится на 2.
Вынести общий множитель 2 за скобки;
8х⁴ - 8х² + 2 = 2(4х⁴ - 4х² + 1). Полученное выражение при любых целых значениях х делится на 2.в) Докажите, что при любых действительных значениях x многочлен не может принимать отрицательных значений.
После вынесения общего множителя 2 в скобках будет квадрат суммы, который больше 0 при любом значении
2(4х⁴ - 4х² + 1) = 2(2х² + 1)².
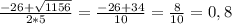

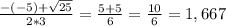

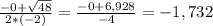
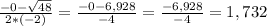
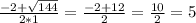
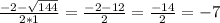
2
= sin(2*15) = sin30 = 1 = 1/4
2 2 2*2
б) (cos(π/8) + sin(π/8)) (cos³(π/8) - sin³(π/8)) =
=(cos(π/8) + sin(π/8))(cos(π/8) - sin(π/8))(cos²(π/8)+cos(π/8) *sin(π/8)+sin²(π/8))= =(cos²(π/8) - sin²(π/8)) (1 + 2sin(π/8) cos(π/8)) =
2
= cos(2 * (π/8)) * (1 + sin(2 * (π/8))) =
2
= cos(π/4) * (1 + sin(π/4)) =
2
= √2 ( 1 + √2 ) = √2 (4 + √2) = 4√2 + 2 = 2 (2√2 + 1) = 2√2 +1
2 2*2 2 4 2*4 2*4 4
в) 1+tgα tg2α = 1
cos2α
1+tgα tg2α = 1 + sinα * sin2α = 1 + sinα * 2sinα cosα =
cosα cos2α cosα cos2α
= 1 + 2sin²α = cos2α + 2sin²α = cos²α - sin²α + 2sin²α =
cos2α cos2α cos2α
= cos²α + sin²α = 1
cos2α cos2α
1 = 1
cos2α cos2α
Что и требовалось доказать.