Объяснение:
24.121
я, конечно прощения, но члены арифметической прогрессии обозначаются как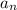 
(у вас это 
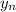) а разность арифметической прогрессии обозначается как b (у вас это d) я буду обзначать так, как принято в математике
1)
а₁₀ = -19
d= -2
применим формулу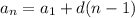 
a₁₀ = a₁ + (-2)*9 = -19 a₁ = -19 +18 = -1
2)
применим ту же формулу
a₅ = a₁ +4d = 13 ⇒ a₁ = 13-4d
a₁₆ = a₁ + 15d = 46 подставим сюда a₁ = 13-4d получим
13-4d +15d = 46 ⇒ 11d = 33 ⇒ d = 3
тогда
a₁ = 13-4d = 13 - 12 = 1
24.123
всё та же формула
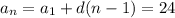
8 +3(n-1) = 24
8+3n -3 = 24
3n = 24-5 = 17 здесь нет целого решения для n ⇒ 24 не есть член арифметической прогрессии
Записываем формулу для вычисления абсциссы вершины параболы:
хв= (по условию)
ув=-8
Так как парабола пересекает ось ординат в точке (0,10), то коэффициент c=10
Уравнение кв функции :
y=ax2+bx+c
Подставляем известные значения
-8=36a+6b+10
36a+6b=-18
6a+b=-3
Но в то же время, из уравнения хв, -b/2a=6
то есть b=-12a
Подставляем:
6a-12a=-3
a=1/2
Тогда
b=-12*1/2=-6
В итоге получаем:
y=1/2 x2-6x+10
Строим по точкам.