Предлагаю для начала решить уравнение:
(3x² + 2x - 1)/(x + 1) = 5
ОДЗ: x + 1 ≠ 0
x ≠ -1
(3x² + 2x - 1)/(x + 1) * (x + 1) = 5 * (x + 1)
3x² + 2x - 1 = 5 * (x + 1)
3x² + 2x - 1 = 5x + 5
3x² + 2x - 5x - 1 - 5 = 0
3x² - 3x - 6 = 0
D = (-3)² - 4 * 3 * (-6) = 9 + 72 = 81
x₁,₂ = (3 ± √81)/(2 * 3) = (3 ± 9)/6
x₁ = (3 + 9)/6 = 12/6 = 2
x₂ = (3-9)/6 = -6/6 = -1 (посторонний корень, не соответствует ОДЗ).
ОТВЕТ: x = 2.
Отвечаю на Ваш вопрос.
В дробно-рациональных уравнениях (подобных данному) нужно избавляться от знаменателя. Он никуда автоматически не пропадает. Просто все уравнение имеют такую особенность, что если умножить обе чести уравнения на одно и то же число (или выражение), то корни уравнения остаются прежними. В таком случае чтобы "исчез" знаменатель (то есть чтобы от него избавиться) обе части уравнения умножают на общий знаменатель (вторая строчка решения, не учитывая ОДЗ).
![sin2x + 2sinx = 1 + cosx\\2sinxcosx+2sinx=1+cosx\\2sinx(1+cosx) = 1 + cosx\\(2sinx-1)(1+cosx) = 0\\sinx = \frac{1}{2} = x = (-1)^n\frac{\pi}{6} + \pi n, n \in Z\\ cosx = -1 = x = \pi + 2\pi m, m \in Z\\x \in [-4;-3]\\-4 < (-1)^n\frac{\pi}{6} + \pi n < -3\\-24 < (-1)^n\pi+6\pi n < -18\\](/tpl/images/1359/4064/d08e0.png)
Подставляем n = 0 - неравенство не выполнено. n = 1 - неравенство не выполнено. Следовательно, при n ≥ 0 решений не будет, т.к. (-1)^n + 6n - функция возрастающая.
Пусть n = -1, тогда выражение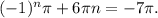 
Так как 3.14 < π < 3.15, то
-22.05 < -7π < -21.98. Очевидно, оно попадает на промежуток (-24; -18). Значит, при n = -1 решение есть на данном отрезке. Подставим n = -1 в серию корней:
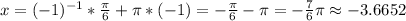
Такими же рассуждениями приходим к тому, что n ≤ -2 так же не являются решениями.
Теперь рассмотрим вторую серию корней:
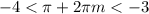
Тут совсем все просто: при m = 0, очевидно, неравенство не выполнено. При m = 1 так же. Так как выражение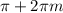 
при возрастании m увеличивается, то и m ≥ 2 также не подходят.
Пусть m = -1, тогда:
Очевидно, что это так. Подставляя m = -2 понимаем, что число меньше -4.
Вопросы ниже в комменты.
ответ: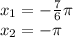 
Объяснение:
Разложить число на простые множители значит записать число как произведение простых чисел .
Простым числом называют натуральное число , делящееся только на себя и на единицу. Составным числом называют число, имеющее больше двух различных делителей Например, числа 2,3,5,7, – простые, а числа 6(2*3),8(2*4),9(3*3) – составные.
Число 388 , оканчивается на 8 значит делится на 2
388:2=194, оканчивается на четное , значит также делится на 2
194 :2= 97 ,вспомним признаки делимости на 3 и 9 , число делится если сумма его цифр делится на 3 или 9.На четыре делится если 2 его последние цифры нули или образуют число которое делится на 4, На пять делится если число оканчивается на 5 или 0.осталось число 6 и 8. На 6 делится если одновременно делится на 2 и 3 , и число делится на 8, если три его последние цифры - нули или образуют число, которое делится на 8.
97=9+7=16, ни на одно число не делится, кроме 1 и самого себя значит 97 это простое число.
388=2*2*97
Число 2520
2520:2= 1260 ( признак делимости на 2)
1260:2=630 ( признак делимости на 2)
630:2=315 ( признак делимости на 5)
315:5=63 ( признак делимости на 3 и 9; 6+3=9 делится и на 3 и на 9
63:3=21 (2+1=3, признак делимости на 3 )
21:3=7 ( неделимое, простое число)
2520 = 2*2*2*3*3*5*7
2) Чтобы обратить обыкновенную дробь в десятичную, нужно числитель разделить на знаменатель.
3 2/5=17/5=17:5=3,4 мы получили конечную десятичную дробь, поскольку в знаменателе обыкновенной дроби стоит 5 ( получить конечную десятичную дробь можно если знаменатель обыкновенной дроби содержит простые множители 2 и 5)
43/30=43:30=1,4 33333… = 1,4(3), поскольку знаменатель обыкновенной дроби содержит кроме 2 и 5 еще 3, то она не может быть представлена конечной десятичной дробью.