1)Степень некоторого числа с отрицательным (целым) показателем определяется как единица, делённая на степень того же числа с показателем, равным абсолютной величине отрицательного показателя: а – n = ( 1 / an )
2)Степень любого ненулевого числа с нулевым показателем равна 1:
a^0 = 1
Например: 2^0 = 1, (-5)^0 = 1, (3 / 5)^0 = 1
3)При умножении степеней с одинаковыми основаниями основание остаётся без изменений, а показатели степеней складываются.
am · an = am + n ,
где «a» — любое число, а «m», «n» — любые натуральные числа.
Пример:
b · b2 · b3 · b4 · b5 = b 1 + 2 + 3 + 4 + 5 = b15
1) Скорость пасс. поезда равна 465/10,5=4650/105=310/7 км/час.
Скорость тов. поезда равна 465/12=155/4=38,75 км/час .
Пусть до встречи пасс. поезд х км, тогда товарный - (465-х) км.
Время, которое ехал до встречи пасс. поезд, и время, которое до встречи ехал тов. поезд одинаково и равно
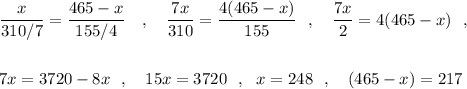
ответ: пасс. поезд проехал 248 км, а тов. поезд проехал 217 км .
2) Скорость 1 спортсмена равна 100/12 м/с , а второго - 100/13 м/с .
Пусть до встречи 1 спортсмен пробежал х м, тогда 2 спортсмен пробежит (200-х) м .
Время, которое спортсмены бежали до встречи одинаково, поэтому
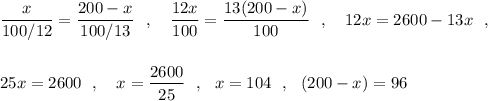
ответ: 1 спортсмен пробежал 104 м , а 2 спортсмен пробежал 96 м .
6а(2) + а + 18а + 3 +6а(2) - а - 18а + 3