1.
1) = ax+ay
2) = 6ax+3bx
3) = 30x^2+15xy
4) = -30b+12a
5) = bx-by
6) = 6xy-2y^2
7) = -12ab-6a^2
8) = 8m^2+8mn
2.
1) = a(4+3a)
2) = -10(2m-3n)
3) = 5a(a-3)
4) = -3x(2y-3x)
5) = 0,5x(x^2-5)
6) = 4y(2x-y)
7) = -mn(mn+1)
8) = 9q^3(2p-q)
1.Пусть тракторов x, тогда комбайнов (х-23),зная что всего было напраленно 187 тракторов
Сос. ур.
1)x+(x-23)=187
x+x-23=187
2x-23=187
2x=210
x=105-тракторов
2)105-23=82-комбайнов
2. пусть х первое число, тогда х+11 второе число.
по условию задачи сумма двух 104, поэтому
х+х+11=104
2х=104-11
2х=93
х=46,5
значит первое число 46,5, а второе 57,5
3. Пусть основание равнобедренного треугольника - х см. Тогда боковые стороны равны х-11 см.
Периметр треугольника - это сумма всех сторон треугольника. Значит, составим уравнение:
68 = х + 2( х - 11 )
68 = х + 2х - 22
3х = 68 + 22
х = 90 : 3
х = 30
Значит, основание равнобедренного треугольника равно 30 см
ответ: x = -π/4 + πn; x = 3π/4 - arcsin(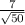
) + πn, n ∈ Z
Объяснение:
0,5sin(2x) + 7cos^2(x) - 3,5 + 3,5 = 3
0,5sin(2x) + 3,5cos(2x) = -0,5
sin(2x) + 7cos(2x) = -1
Разделим обе части на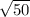 
Получаем:
Пусть sin(α) = 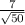, тогда cos(α) =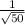 
α = arcsin()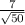
Получаем уравнение sin(2x)*cos(α) + sin(α)*cos(2x) = -cos(α)
Применяем формулы синуса суммы и формулу приведения
sin(2x + α) = -sin(π/2 - α)
sin(2x + α) = sin(α - π/2)
1) 2x + α = α - π/2 + 2πn
x = -π/4 + πn, n ∈ Z
2) 2x + α = π + π/2 - α + 2πn
x = 3π/4 - α + πn
x = 3π/4 - arcsin(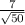) + πn, n ∈ Z
1) (х+y)a=а(х+у)=ах+ау
2) 3x(2a+b)=6ах+3bx
3) 5x(6x+3y)=30x²+15xy
4) -6(5b-2a)=-30b+12a=12a-30b
5) b(x-y)=bx-by
6) 2y(3x-y)=6xy-2y²
7) 3a(-4b-2a)=-12ab-6a²=-(12ab+6a²)
8) 8m(m+n)=8m²+8mn
2. Вынесите за скобки общий множитель.
1) 4a+3a²=a(4+3a)
2) -20m+30n=-10(2m-3n) -20m+30n=30n-20m=10(3n-2m)
3) 5a²-15a=5a(a-3)
4) -6xy+9x²=-3x(2y-3x) -6xy+9x²=9x²-6xy=3x(3x-2y)
5) 0,5x³-2,5x=0,5x(x²-5)
6) 8xy-4y²=4y(2x-y)
7) -m²n²-mn=-mn(mn+1)
8)18pq³-9q⁴=9q³(2p-q)