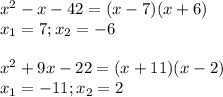
x ∈{-2} ∪ [2;7]
Объяснение:
1) Найдём нули функции у₁ = х²-5х-14:
х²-5х-14 = 0
х₁,₂ = 5/2 ± √(25/4 +14) = 5/2 ± √(81/4) = 5/2 ± 9/2
х₁ = 5/2 + 9/2 = 14/2 = 7
х₂ = 5/2 - 9/2 = - 4/2 = -2
Графиком функции у₁ = х²-5х-14 является парабола, ветви которой направлены вверх; следовательно, у₁ = х²-5х-14 ≤0 на участке
x ∈ [-2; 7].
2) Неравенство х² ≥ 4 эквивалентно неравенству: х²- 4 ≥ 0.
Найдём нули функции у₂ =х²- 4:
х²- 4 = 0
х² = 4
х = ± √4
х₃ = - 2
х₄ = 2
Графиком функции у₂ = х²- 4 является парабола, ветви которой направлены вверх; функция у₂ = х²- 4 больше или равна нулю на участках:
x ∈(-∞; -2] ∪ [2;+∞)
3) Объединяем полученные решения, для чего на числовой оси отмечаем точки х₂ = -2; х₃ = -2; х₄ = 2; х₁ = 7 и находим перекрываемые области значений, одновременно удовлетворяющие неравенству х²-5х-14 ≤ 0 и неравенству х² ≥ 4:
x ∈{-2} ∪ [2;7]
ответ: x ∈{-2} ∪ [2;7]
ответ
1
Helper211
ответ: 0,88
Пошаговое объяснение:
Формула для приближенного вычисления значения функции в точке с дифференциала: f(x)=f(a+dx)≈f(a)+f'(a)dx
где x - заданная точка,
a - вс точка, в которой удобно вычислять значение функции и производной,
dx - разность между заданной точкой и вс
Ближайшая к 0,96 точка, где легко вычислить значение функции и ее производной, это 1 (в данном случае функция - ).
dx = x - a = 0,96 - 1 = -0,04
f(a) = f(1) = 1;
f'(x)=
f'(a)=f'(1)=3;
f(x)=f(a+dx)≈f(a)+f'(a)dx:
Объяснение:
D=b^2-4ac=1+168=169.169 под корнем это 13
x1=7.
x2=-6.
б)x^2+9x-22=0
D=81+88=164.