Нужное рациональное число лежит на отрезке [√2 ; √3], поэтому оно положительное, а значит его можно представить как  , где
, где 

Берём любое натуральное n, приводим границы двойного неравенства к общему знаменателю и вспоминаем, квадраты каких натуральных чисел лежат на нужном промежутке.

Получается дробь 
Таким образом можно получить

ответ: 1,5.
задание 9
пусть ширина х,тогда длина х+0,25х составим уравнение
х+х+0,25х=54:2
2,25х= 27
х=27:2,25
х=12 см ширина
12+12*0,25=12+3=15 см длина
12*15= 180 кв см площадь
задание 10
1)сумма восьми чисел 5,2*8= 41,6
пусть искомое число х,составим уравнение
41,6+х=5,7*9
41,6+х=51,3
х=51,3-41,6
х= 9,7 искомое число
задание 5 ответ: х= - 0,5
задание 4 ответ: вариант 2
задание 8
/4х/=5,6
решение разбивается на отдельные случаи
случай 1
4х=5.6
х=5,6:4
х= 1,4
случай 2
- 4х=5,6
х=5,6:(-4)
х= - 1,4
ответ х=1,4;х=-1,4
Всего трехзначных чисел: 999 - 99 = 900 из них выбираем числа, которые делятся на 6.
Наименьшее число, делящееся на 6: 102, а наибольшее — 996
Последовательность чисел делящихся на 6 такова: 102; 108; .... ; 996 - арифметическая прогрессия (каждый член прибавляется число 6)
По формуле n—го члена арифметической прогрессии вычислим количество трехзначных чисел, делящихся на 6
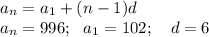
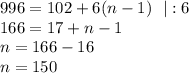
A — Вася выбирает наугад трехзначное число.
Количество всевозможных исходов: n(Ω) = 900
Количество благоприятных исходов: n(A) = 150
По формуле классической вероятности: 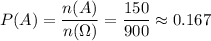
Объяснение:
Напрямую через калькулятор.
√2 ≈ 1,414; √3 ≈ 1,732.
Между ними есть числа 1,5; 1,6; 1,7.
Алгебраическим решением
√2 < √2,25 = 1,5
√3 > √2,89 = 1,7
Между √2 и √3 есть числа 1,5; 1,6; 1,7.