1. область определения х принадлежит (-бесконечность;+бесконечность).
2. пересечение с осью ординат (ОУ): x=0 f(x)=-1
3. исследование функции на четность/нечетность:
f(x)=x^3-2x^2+x-1
f(-x)=-x^3-2x^2-x-1 функция не является ни четной ни нечетной
4. производная функции:
3х^2-4x+1/
нули производной:
х=1/3. х=1.
5. Функция возрастает. х принадлежит (-беск.;1/3] U [1/3;+беск).
функция убывает. х принадлежит [1/3;1]
6. минимальное значение функции. -бесконечность
максимальное значение функции +бесконечность
Объяснение:
Построить график функции
у=2×|х|+3
Шаг 1.
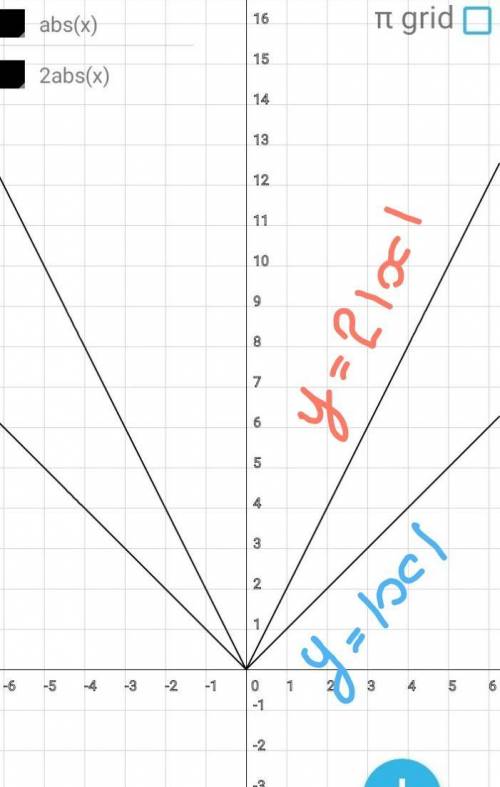
Строим график функции
у=|х|
Графиком являются биссектрисы
1 и 2 координатных четвертей.
Весь график расположен в верхней
полуплоскости.
Шаг 2.
Нужно изменить угол наклона вет
вей графика.
Построим и заполним таблицу:
у=2×|х|
х 0 -2 2
у 0 4 4
Строим график фунеции
у=2×|х|.
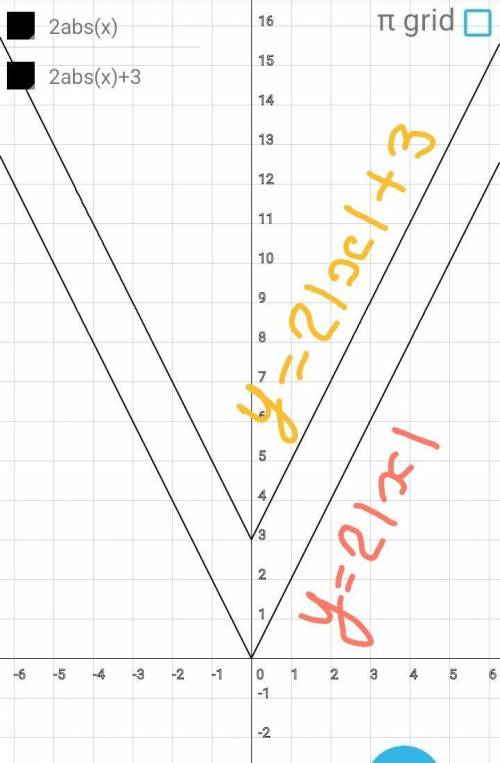
Шаг 3.
Строим график функции
у=2×|х|+3
График функции у=2×|х| поднимаем
вверх на 3 единицы ( совершаем па
раллельный перенос вдоль положи
тельного направления ОУ на 3ед. от
резка).
Построен искомый график.
Находим расстояние по формуле - s=v*t
1) 90км/ч * х
2) 60 км/ч * (х+1,5)
Так как расстояние одинаковое, приравниваем их
90км/ч * х= 60км/ч * (х+1,5)
90х=60х+90
90х-60х=90
30х=90
Х=3(ч)
90*3=270 км