Объяснение:
так, рассмотрим этот пример:
Пример 3, упростить выражение:
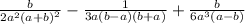
здесь, автор пытался донести, что нам нужно домножить на определенные числа, дабы получить общий знаменатель 6а³(а-b)(a+b)²
При этом, он имел ввиду, что умножение на второй знаменатель можно произвести по разному:
1) если использовать общий множитель
6а³(b-a)(a+b)² , то домножить нужно на 2а²(а+b), и это действительно не принципиально, но тогда третий множитель будет "страдать" - нужно будет домножить его уже со знаком "-": -(a+b)², чтобы при умножении, как вы и сказали: (а-b) = -(b-a) и при умножении двух минусов, мы получаем знак "+"
, так и наоборот для второго случая:
2)если использовать общий множитель
6а³(а-b)(a+b)² , то домножить второй знаменатель нужно на -2а²(а+b)!
А третий на (a+b)², с плюсовым перед стоящим знаком.
И не забываем так же про первый знаменатель :)
Тут всё дело в том, какой общий множитель вы захотите использовать.
Надеюсь, понятно объяснил.
Объяснение:
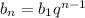решаем по этой формуле (1)
q - знаменник
131 - 1) 32 = 108q³ ⇒ q³ = 8/27 ⇒ q = 2/3
131-2) b₃ = 
⇒ q = √5
132. 7-4 = 3 ⇒ c₇ = c₄*q³ ⇒ q³ = -320/40 = -8 ⇒ q = -2 ⇒ c₁ = c₄/q³ = 40/8 = 5
133. b₁ = 3/4, q = 2
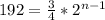
n-1 = 8
n = 9
134. 48, 48q, 48q², 48q³, 243 ⇒ 243 = 48q⁴ ⇒ q⁴ = 243/48 = 81/16 ⇒ q = 3/2 = 1.5
48, 72, 108, 162, 243 вот жирным выделены эти ТРИ числа
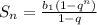(2)
135-1) из ф-лы (1): 280= b₁5³ ⇒ b₁ = 280/125 = 56/25
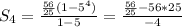
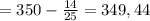
135-2) из формулы (1) 4√2 = q⁴ *√2 ⇒ q = -√2 Т. к. по условию q <0
из (2)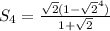 
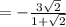или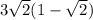 
6cos^2(5x)+5cos(5x)-1=0
Замена: cos(5x)=a
6a^2+5a-1=0
D=25+4·6=25+24=49.
a1=(-5-7)/12=-1
a2=(-5+7)/12=1/6
Обратная замена:
cos(5x)=1/6
cos(5x)=-1
5x=±arccos(1/6)+2пn, nєZ.
5x=п+2пn, nєZ.
x=±1/5·arccos(1/6)+2/5пn, nєZ.
x=п/5+2/5пn, nєZ.
ответ: ±1/5·arccos(1/6)+2/5пn, nєZ или x=п/5+2/5пn, nєZ.