х'2+4х-5>0
Решение дискриминантом. Формула дискриминанта: b'2 - 4ac. Соответственно:
16-4х1х(-5) = 16+20 = 36. Корень 36 - 6.
Х1 = (-b+-корень) деленное на 2хa.
Х1 = (-4+6):2 (дробь) = 1
Х2 = (-4-6):2 (дробь) = -5
Рисуем координатную прямую (как я ее называю) и отмечаем там две точки, х1 и х2 соответственно.
+ - +
-51>
Расставляем плюсы и минусы над координатной прямой. С права на лево. До единицы будет плюс, между единицей и -5 будет минус, после -5-ти будет плюс. Смотрим в начальное задание, знак был больше, значит закрашиваем промежутки где стоит плюс(засечками наклоненными). И конечный ответ: (-знак беск. ; -5) U (1;+знак беск)
Вроде верно. Удачи1
⊥ 
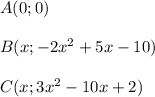
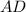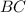
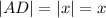, так как ![x \in [0,6;1,5]](/tpl/images/1360/8622/6d679.png)
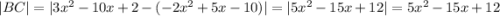
так как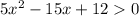 
при любых х, D=225-240<0
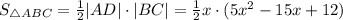- функция, зависящая от х.
Исследуем на наибольшее и наименьшее значение на ![[0,6;1,5]](/tpl/images/1360/8622/d089f.png)
⇒ 
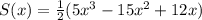
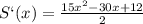
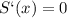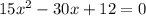
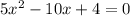
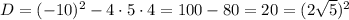
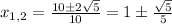
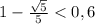так как 
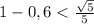и возводя в квадрат получим:
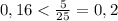
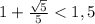так как 
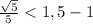и возводя в квадрат получим:
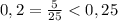
Значит только одна точка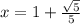 
возможного экстремума принадлежит данному отрезку [0,6;1,5]
Эта точка - точка минимума, так как при переходе через точку производная меняет знак с - на +
Значит наименьшее значение площади
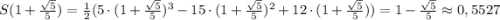
Наибольшее значение на одном из концов отрезка:
при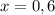 
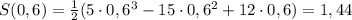- наибольшее значение
при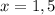 
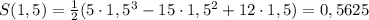
О т в е т. Наибольшее значение площади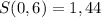 
наименьшее значение площади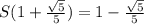 
-12х+8х>56+4-20
-4x>40
-x>10
x<-10
2) -16x-114>-30x-35-9
-16x+30x>-35-9+114
14x>70
x>5
3) 9-6x-36<12x+27
-6x-12x<27+36-9
-18x<54
18x>-54
x>-3
4) 110-18x≥9-6x-7
-18x+6x≥2-110
-12x≥-108
x≤9
5) 25-30x+2≤-16x-57
-30x+16x≤-57-27
-14x≤-84
x≥6
6) -36x-42-6≤-30x-48
-36x+30x≤-48+48
-6x≤0
x≥0